Raggi acustici in mare: curvatura strato isotermo

Caso tipico di doppia curvatura dei raggi acustici: si generano zone d'ombra non illuminate dal suono ( sezione grigia )

Dall'andamento delle traiettorie dei raggi acustici in mare dipendono le capacità di scoperta dei sonar.

Le diverse situazioni che si possono verificare a seguito dei molteplici andamenti delle traiettorie dei raggi acustici si estendono dall'impossibilità di qualsiasi rilevamento sonar, nelle zone d'ombra, alle capacità di scoperta dei bersagli a distanze eccezionali nei casi di canalizzazione del suono.

Per queste ragioni lo studio dell'andamento delle traiettorie dei raggi acustici in mare risulta di primaria importanza nella conduzione del sonar.

Gli esercizi svolti a titolo d'esempio, nella voce, sono stati estrapolati dal testo "FONDAMENTALS OF SONAR" di J.W.Horton traducendo le formule di calcolo in routine software.

La curvatura dei raggi acustici in mare

I raggi acustici dovuti all'energia emessa in mare da una sorgente di suono sono soggetti a curvatura dovuta a due cause diverse:

• la prima, più significativa, dipende dalla variazione della velocità del suono in funzione della temperatura dell'acqua con la profondità e da altre cause minori.

• la seconda, meno rilevante, dipende dalla variazione della velocità del suono dovuta alla densità del mezzo in funzione della profondità; in questo caso si considera costante la temperatura nell'intervallo di quota interessato ai computi.

Entrambe le situazioni sono governate dalla legge di Snell:

$\left(\frac{\cos {\delta }_1}{c_1}\right)=\left(\frac{\cos {\delta }_2}{c_2}\right)$

figura 01

La legge di Snell è illustrata in modo semplice nel grafico di figura 01 dove, invece di una curva, è mostrata una spezzata:

Dalla figura si vede che nel tratto di mare compreso tra quota $Z=0$ e quota $Z=100$ m la velocità del suono è di $c_1=1480$ m/S. ed il raggio acustico indicato in celeste si sviluppa secondo l'inclinazione ${\delta }_1$, una volta raggiunta la quota $Z=100$ m il raggio s'immette nel tratto di mare compreso tra $Z=100$ m e $Z=200$ m dove la velocità del suono e di $c_2=1440$ m/S. in questo tratto il raggio assume l'inclinazione ${\delta }_2$ come mostra il tratto viola.

In questo esempio è ipotizzata, ad arte, una variazione della velocità del suono a scalino, in realtà la variazione della velocità del suono in mare è continua e genera andamenti dei raggi acustici dal percorso curvilineo.

Dalla legge di Snell derivano gli algoritmi per il tracciamento dei raggi acustici in mare illustrati nella presente voce.

Le grandezze delle variabili utilizzate nelle fasi di calcolo a seguire

Le grandezze utilizzate per le computazioni sono espresse con unità di misura anglosassoni:

Temperature: (°F ) in gradi Fahrenheit ( °F = °C x 9/5 + 32 )

Profondità: (ft) in feet ( ft = mt x 3.281 )

Distanze: (yd) in yard ( yd = m x 1.094 )

Gli angoli, in grandezza universale, sono espressi in radianti

L'obiettivo dei calcoli

I calcoli hanno come obiettivo la valutazione di n coppie di coordinate in grado di consentire il tracciamento di una curva, la traiettoria del percorso del suono, che si sviluppa secondo una o più archi di circonferenza così come indicato in figura 1.

In questo particolare procedimento l'ascissa $(S)$ , distanza dalla sorgente acustica espressa in yard, è la variabile dipendente mentre l'ordinata $(D)$, variabile indipendente, è la profondità dei punti di calcolo in feet.

L'arco denominato " angolo di radenza" è l'angolo formato tra la tangente del cerchio e un segmento parallelo all'asse delle ascisse passante per il punto di tangenza.

La valutazione del valore di quest'angolo è fondamentale nel definire l'andamento della $S=f(D).$

Per ciascuna coppia di coordinate il valore della variabile $D$ è stabilito dall'operatore mentre il valore di $S$ ne è una funzione : $S=f(D).$

Più elevato è il numero delle coppie più punti definiscono la traiettoria.

I calcoli devono essere eseguiti a 9 decimali.

Variazione della temperatura dell’acqua in funzione della profondità

figura 2

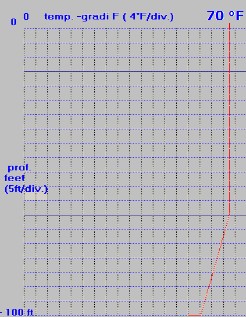
Prima d’iniziare il percorso di calcolo accennato è utile mostrare il grafico di figura 2, detto batitermogramma, che mostra, in questo caso specifico, come varia la temperatura dell’acqua in mare, misurata con batitermografo, in funzione della profondità e di conseguenza come varia con la temperatura, la velocità del suono

Lo strato isotermo si estende, con un tratto verticale, dalla superficie del mare a $65$ feet a seguire, con un tratto inclinato, la temperatura decresce con l'aumentare della profondità.

Dal grafico assumeremo, nello strato isotermo, la temperatura T = 70 °F da utilizzare pe il calcolo della velocità del suono che n'é una variabile.

Procedura di calcolo nello strato a temperatura costante

Il calcolo di $S=f(D)$ mira alla determinazione delle coordinate dei punti della traiettoria $D;S(D)$, ed è svolto secondo i seguenti passi:

• p0- si assumono un numero di valori ($D$) (ordinate dei punti della traiettoria) necessari alla definizione del tracciato

• p1- si assume il gradiente di velocità del suono nello strato isotermo pari a: $(g1)=0.0182$ (la velocità del suono. nello strato isotermo, varia soltanto in funzione della pressione con la quota)

• p2- si stabilisce di collocare il trasduttore alla prof. di $15ft$ (valore utilizzato per i trasduttori nelle navi di superficie)

• p3- si fissa un valore della temperatura $(T)$ dell'acqua

• p4- si fissa la salinità $(sa)$, in parti per mille, in base ad ipotesi realistiche

• p5- si stabilisce la profondità $(d1)$ dello strato nel quale eseguire i calcoli (quota del trasduttore)

• p6- si calcola il valore della velocità del suono $C$ alla quota del trasduttore

• p7- si calcola il raggio $(r1)$ dell'arco di cerchio che forma la traiettoria

• p8- si calcola $\cos \theta$ ; coseno dell'angolo di radenza

• p9- si ricava l'angolo $\theta$

• p10- si calcola infine $S=f(D)$ con l'espressione: $S=[r1\cdot \mathrm{sen}(z)]/3$

Le funzioni di calcolo

Algoritmi per il calcolo dell’ascissa $S(D)$:

L'ascissa si computa con $S=[r1\cdot \mathrm{sen}(z)]/3$

Dove:

$z=\arccos \theta$

$\theta$ = angolo di radenza

$\cos \theta =(1+Dd)/r1$ (coseno dell’angolo di radenza)

$r1=(C/g1)$ (raggio della traiettoria)

$C=4411+(11.25)\cdot (T)-0.045\cdot (T^2)+g1\cdot d1+4.3\cdot (sa-34)$ velocità del suono in corrispondenza del trasduttore, dove:

$T$ = temperatura nello strato isotermo

$g1$ = gradiente di velocità nello strato isotermo

$d1$ = quota del trasduttore

$sa$ = salinità nello strato

Applicazione delle funzioni di calcolo

In questo esercizio consideriamo un raggio acustico orizzontale emesso dal trasduttore avente, ovviamente, l'angolo di radenza $\theta =0$, assumeremo inoltre per la temperatura costante nello strato il valore $T=70$°F indicato in figura 3.

Si voglia calcolare la coppia di coordinate $D;S(D)$ di un punto della traiettoria per $D=10$ ft (variabile indipendente)

$d1=15$ ampiezza dello strato isotermo (da 0 a 15 ft), dalla superficie al trasduttore d’emissione

$g1=0.0182$ gradiente assunto per la strato isotermo

$Dd=D-d1$ = $-5$

$Sa=35$ parti per mille

$T=70^{\circ }F$

$C=4411+(11.25)\cdot (70)-0.045\cdot (70^2)+0.0182\cdot 15+4.3\cdot (35-34)$ = $4982$ ft/s.

$r1=4982/0.0182$ = $273736$ yd

$\cos \theta =1-4/273736$ = $0.99998173$

$z=\arccos (0.99998173)$ = $0.006044842$

$S=(273736\cdot \sin (0.00604442)/3$ = $551$ yd

Queste le coordinate del punto:

$D=10$ ft ; $S=551$ yd

Il tracciamento della traiettoria

figura 3

Per una presentazione grafica della traiettoria del raggio acustico si dovrebbero ripetere i calcoli precedentemente fatti per un numero molto elevato di coordinate $D;S$ pur non ottenendo una soddisfacente presentazione dell'arco di curva.

Il problema si risolve con l'impiego di un eseguibile di calcolo sviluppato in Visual Basic; si tratta di una routine impostata secondo gli algoritmi illustrati in precedenza in grado di eseguire le computazione a passi di piccole frazioni della variabile indipendente $D$.

Il risultato dell’utilizzo dell’eseguibile è mostrato in figura 3 dove a sinistra del tracciato del raggio acustico è disposto il grafico dell'andamento della temperatura già illustrato in figura 2

La variabile indipendente $D$ decresce da $D=15$ a $D=0$ feet, la funzione $S(D)$ cresce da $S=0$ a $S=880$ yard

Sulla curva è evidenziato con un cerchietto rosso il punto calcolato nell'esercizio precedente; $D=10$ feet e $S=551$ yard.

Nel valutare visivamente il tracciato si deve osservare che l'accentuata curvatura del raggio acustico dipende dalla differenza di scala tra le coordinate: $D$ è in feet mentre $S$ è in yard.

L’eseguibile di calcolo

figura 4

Come accennato in precedenza sull'utilizzo di un eseguibile di calcolo se ne propone l’impiego scaricandolo all'indirizzo riportato nella sezione Collegamenti esterni

Il programma di calcolo consente, oltre il tracciamento della curva di figura 3, anche la possibilità di eseguire calcoli per punti illustrando in tal modo tutto il processo manuale di elaborazione numerica svolto in precedenza presentando un tabulato con funzioni e dati così come riportato in figura 4.

Bibliografia

G.Pazienza, Fondamenti della localizzazione marina, La Spezia, Studio grafico Restani, 1970.

W. Horton, Foundamentals of Sonar, United States Naval Institute,Annapolis Maryland, 1959

A. De Dominics Rotondi, Principi di elettroacustica subacquea , Elettronica San Giorgio-Elsag S.p.A., Genova, 1990.

C. Del Turco, Sonar- Principi - Tecnologie – Applicazioni , Tip. Moderna La Spezia, 1992

Collegamenti esterni

Wikiraggiisotermo

o su

raggiisotermo