Campionamento di segnali analogici

Template:Risorsa Partendo da un segnale limitato, nell'ipotesi di campionamento e ricostruzione ideali, l'operazione di campionamento è reversibile; di conseguenza, a partire dalla sequenza di campioni di un segnale, è possibile risalire al segnale analogico di partenza. Al contrario, nel caso di campionamento e ricostruzione operati con filtri reali, è necessario valutare la distorsione introdotta da alcune non-idealità, modellizzabili come operazioni lineari e tempo-invarianti.

Campionamento ideale

Studiamo il campionamento ideale, con passo uniforme. Si tratta di estrarre, a partire dal segnale analogico $x_a(t)$, i valori che questo assume negli istanti $n\cdot T_c$, con $n\in \mathbb{N}$.

Nel caso in esempio, abbiamo $T_C=1$. Si ha

$x_c[n]={\{x(n\cdot T_C)\}}_{n=-\mathrm{\infty }}^{+\mathrm{\infty }}$

Uno strumento utile per formalizzare questo passaggio è la delta di Dirac, che gode della proprietà

$x(t)\cdot \delta (t-t_0)=x(t_0)\cdot \delta (t-t_0)$

Si usa, quindi, la delta di Dirac come operatore di cattura $\delta$ Ripetendo l'operazione di cattura per tutti gli $n\cdot T_C$, si ha

$x_c(n\cdot T_C)=x(n\cdot T_C)\delta (t-n\cdot T_C)$

che è una $\delta$ con ampiezza infinita, ma che contiene nell'area il valore $x(n\cdot T_C)$ cercato.

Si definiscono il tempo di campionamento $T_C$ e la frequenza di campionamento

$f_C=\frac{1}{T_C}$

Il segnale campionato viene definito come

$x_c(t)=\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}x(k\cdot T_C)\delta (t-k\cdot T_C)$

Bisogna notare che $x_c(t)$ è un segnale definito sull'asse dei tempi, non è un segnale discreto. Definiamo il pettine di impulsi di Dirac ${\delta }_{T_C}$ con

${\delta }_{T_C}=\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}\delta (t-k\cdot T_C)$

dove ogni impulso è in posizione multipla di $T_C$ ed ha area unitaria. Otteniamo, allora, il modello del campionatore ideale,

Questo campionatore è un sistema

• lineare, cioè vale il principio di sovrapposizione degli effetti;
• tempo variante, cioè non è possibile disegnare la risposta in frequenza, dal momento che l'uscita del sistema dipende fortemente dall'istante di tempo in cui esso viene applicato.

Il campionatore ideale non è un sistema LTI (lineare e tempo-invariante), infatti genera nuove ed infinite armoniche; da questo fatto si deduce che non è possibile disegnare la risposta in frequenza del sistema.

Un risultato importante è che, a partire dal segnale campionato $x_c(t)$ si può risalire al segnale di partenza $x(t)$ senza alcuna perdita di informazione, sotto alcune ipotesi.

Prendiamo un qualsiasi segnale $x(t)$ trasformabile secondo Fourier,

$X(f)=F\{x(t)\}=\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}x(t)e^{-j2\pi ft}dt$

Questo è un integrale improprio, definito nell'intervallo $(-\mathrm{\infty },+\mathrm{\infty })$, per una funzione $x(t)\in ℂ$, perché $x(t)$ potrebbe anche essere complessa. Possiamo calcolare anche la trasformata di Fourier del segnale campionato,

$\begin{array}{cc}{X}_c(f)& =\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}{x}_c(t)e^{-j2\pi ft}dt\\ & =\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}x(t)\cdot {\delta }_{T_C}(t)\cdot e^{-j2\pi ft}dt\end{array}$

Ricordiamo la proprietà della trasformata di Fourier

$F\{x(t)\cdot y()\}=X(f)*Y(f)$

risulta che

$X_c(f)=X(f)*F\{{\delta }_{T_C}(t)\}$

dove si ha

$F\{\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}\delta (t-k{T}_C)\}=\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{1}{T_C}\delta (f-\frac{n}{T_C})$

da cui si ha che

$F\left\{{\delta }_{T_C}\right\}=\frac{1}{T_C}{\delta }_{\frac{1}{T_C}}(f)=F_C{\delta }_{F_C}(f)$

Quello che succede, quindi, è che la trasformata del segnale campionato è la convoluzione tra le trasformate del segnale originale e del campionatore, dove il campionatore, che è un treno di impulsi nel dominio del tempo, diventa un treno di impulsi anche nel dominio delle frequenza, ma gli impulsi hanno altezza riscalata di $\frac{1}{T_C}$ e la distanza tra gli impulsi, invece di essere $T_C$, è a sua volta trasformata in $\frac{1}{T_C}$. Si noti la definizione di frequenza di campionamento

$F_C=\frac{1}{T_C}$

Usando le proprietà delle delta di Dirac $\delta$

$X(f)*\delta (f-f_0)=X(f-f_0)$

si ottiene che

$X_c(f)=\frac{1}{T_C}\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}X(f-\frac{k}{T_C})$

La traslazione nelle frequenze delle varie $\delta$ fa sì che, una volta convolute con $X(f)$, si abbia una ripetizione della trasformata $X(f)$ attorno al punto in cui è centrata la delta: questo fenomeno è sintomo della non-linearità del processo, dal momento che si vengono a creare delle nuove ed infinite armoniche.

La ripetizione dello spettro di $X(f)$, una volta avvenuto il campionamento, è periodica di periodo $F_C$.

Esempio grafico del processo di campionamento

Prendiamo un segnale con la trasformata (in modulo) seguente, $|X(f)|$:

Definiamo la banda del segnale $B$, che nell'esempio è $B=1$; di conseguenza, il segnale utile si sviluppa sul supporto $(-B,B)=(-1,1)$. Per semplicità, abbiamo considerato un segnale $x(t)$ reale, in modo tale da avere aderenza con la realtà ed una trasformata di Fourier pari in modulo. Abbiamo imposto, sempre per semplicità, un segnale a banda limitata, cioè tale che

$X(f)=0\mathrm{\forall }|f|\ge B$

Campionare nei tempi significa replicare la trasformata nelle frequenze:

Nel caso in esame, si hanno delle repliche del segnale originale attorno ai valori

$f=k\cdot F_C\mathrm{\forall }k\in \mathbb{Z}$

dove si è preso $F_C=5$.

Per il Teorema di Shannon, non si hanno sovrapposizioni di segnale se si rispetta la condizione

$F_C\ge 2\cdot B$

cioè, se la frequenza di campionamento è almeno due volte superiore alla banda del segnale, che altro non è che la sua massima frequenza. Rispettando questa condizione, le repliche spettrali del segnale non vanno a sovrapporsi tra loro, quindi non si crea il fenomeno dell'[[w:Aliasing|aliasing].

Per ripristinare il segnale originale, una volta trasmesso il segnale campionato, è sufficiente ripristinare la trasformata originale, il che coincide con l'eliminare le repliche spettrali introdotte dal campionamento. Per fare questa operazione di pulizia, si può utilizzare ad esempio un filtro passabasso ideale, che amplifichi il segnale di un fattore $T_C$.

$H_I(f)=T_C\cdot rect\left(\frac{f}{F_C}\right)$

dove si definisce la funzione rettangolo come

$rect\left(\frac{f}{F_C}\right)=\{\begin{array}{cc}1& |f|<\frac{F_C}{2}\\ \frac{1}{2}& f=\pm \frac{F_C}{2}\\ 0& \text{ altrove }\end{array}$

La funzione $H_I(f)$ è definita come la trasformata del filtro passabasso ideale, con fase nulla.

Questo è definito come il filtro di interpolazione (o di ricostruzione) ideale, dal quale si ottiene

$X_r(f)=X_c(f)\cdot H_I(f)=X(f)$

dove $X_r(f)$ è la trasformata del segnale ricostruito che, nel caso visto, coincide con la trasformata del segnale originale.

Nel dominio del tempo, per la ricostruzione si può applicare la proprietà del prodotto di trasformate, che dice

$x_r(t)=x_c(t)*h_I(t)$

dove si ha

$\begin{array}{cc}{h}_I(t)& =F^{-1}\{H_I(f)\}\\ & =sinc\left(\frac{t}{T_C}\right)\\ & =\frac{\sin \left(\frac{\pi \cdot t}{T_C}\right)}{\left(\frac{\pi \cdot t}{T_C}\right)}\end{array}$

da cui si ottiene che

$\begin{array}{cc}{x}_r(t)& =x_c(t)*h_I(t)\\ & =(\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}x(k\cdot T_C)\delta (t-k\cdot T_C))*sinc\left(\frac{t}{T_C}\right)\\ & =\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}x(k\cdot T_C)sinc\left(\frac{t-k\cdot T_C}{T_C}\right)\\ & =\cdots \\ & =\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}x(k\cdot T_C)\cdot T_C\frac{\sin (\frac{\pi t}{T_C}-\pi k)}{\pi (t-k\cdot T_C)}\end{array}$

Ovviamente, questo risultato è diverso a seconda del tipo di finestra che si usa, questi conti valgono solo con finestra ideale a rettangolo.

Una formula interpolante è

$x(t)=\sum _{n=-\mathrm{\infty }}^{+\mathrm{\infty }}x(n\cdot T_C)\cdot sinc\left(\frac{t-n\cdot T_C}{T_C}\right)$

dove si definisce la funzione sinc come

$sinc(\alpha )=\frac{sin(\pi \alpha )}{\pi \alpha }$

Nel caso in cui non venga rispettato il teorema di Shannon, allora si rischia l'aliasing, cioè, nel momento in cui si va a campionare il segnale originale, si rischia che le varie repliche del segnale vadano a sovrapporti le une con le altre.

In questo esempio, il segnale ha banda $B=1$, mentre la frequenza di campionamento è

$F_C=1,8<2\cdot B=2$

Il risultato del processo di campionamento, quindi, è l'aliasing, o equivocazione frequenziale. Una volta che questo fenomeno entra in gioco, non è più possibile ricostruire il segnale originale, perché non è possibile discriminare la fonte dei segnali che si vanno a sommare.

Nel caso in cui sia fissata la frequenza di campionamento $F_C$, è opportuno inserire nella catena, prima del campionamento, un filtro antialiasing analogico, cioè un filtro di tipo passabasso che limiti la banda del segnale in ingresso, in modo tale da eventualmente distorcere il segnale, ma senza introdurre aliasing nel sistema, un fenomeno peggiore. Si limiterà quindi la banda utile del segnale con un passabasso

$W<\frac{F_C}{2}$

Questa operazione è da fare in ogni caso, anche se il segnale in ingresso è noto avere una banda accettabile per il campionatore; infatti, il filtro antialiasing è in prossimità del campionatore ed è in grado di abbattere in maniera significativa il rumore elettronico introdotto dalla circuiteria che porta il segnale analogico al campionatore; se manca il filtro passabasso, si rischia che troppo rumore entri nel campionatore e vada a sporcare anche il segnale originale, in bassa frequenza.

Ricostruzione del segnale

Abbiamo detto che, per ricostruire il segnale originale a partire dalla sua versione campionata, è sufficiente introdurre un filtro passabasso, detto filtro ricostruttore, o di interpolazione. Il filtro ideale ha per trasformata di Fourier un rect, cioè ha un sinc nei tempi.

Il segnale $h_I(t)$ è un sinc che interseca l'asse dello zero nei punti multipli di $T_C$, cioè

$h_I(t)=0\mathrm{\forall }t=k\cdot T_C\mathrm{\forall }k\in \mathbb{Z}\setminus \{0\}$

Trattiamo il filtro di ricostruzione come un oggetto analogico, quindi ci dobbiamo aspettare che in ingresso ed in uscita ci siano due segnali analogici (conformità di notazione); non posso inserire, nella cascata di filtri, un segnale digitale in ingresso ad un filtro analogico. Si impone quindi l'introduzione di un sistema di trasformazione che prenda i campioni digitali $x[n]$ e li trasformi in un treno di delta di Dirac $\delta$ modulate in area con i campioni $x[n]$: soltanto il segnale in uscita dal ricostruttore analogico potrà poi essere inserito all'interno del filtro di ricostruzione analogico.

L'interpolatore è ideale, perché non introduce disturbo tra un campione e gli altri; infatti, i sinc, opportunamente traslati tra loro, sono dei segnali ortogonali, cioè possono essere usati per definire una base di uno spazio vettoriale.

Questo tipo di ricostruttore è detto PAM a segnale elementare sinc, dove PAM sta per Pulse Amplitude Modulation, cioè modulazione in ampiezza di un impulso elementare, in questo caso il sinc.

Bisogna notare che il sinc ha un supporto infinito, quindi anche il filtro di ricostruzione ha una risposta all'impulso infinita: questo significa che il filtro interpolatore ideale non è fisicamente realizzabile. Tuttavia, se la frequenza di campionamento $F_C$ non è la minima possibile, si hanno dei margini per la semplificazione del filtro di ricostruzione, in modo tale che questo possa avere delle transizioni meno marcate; infatti, se si campiona ad una frequenza maggiore della frequenza minima, si introduce uno spazio tra le repliche dello spettro, permettendo la realizzabilità fisica del filtro.

Nell'immagine d'esempio, considerando una larghezza di banda $B=1$, si ha che l'inizio della replica successiva è alla frequenza

$f=F_C-B=5-1=4$

così come la fine della replica precedente è alla frequenza

$f=-F_C+B=-5+1=-4$

Allora, si potrà avere un filtro di ricostruzione definito come

$H_r(f)=\{\begin{array}{cc}{T}_C& \mathrm{\forall }|f|<B\\ 0& \mathrm{\forall }|f|>F_C-B\\ \text{qualsiasi}& |f|\ge B\text{ e }|f|\le F_C-B\end{array}$

Tipicamente, nei sistemi reali si sceglie una frequenza di campionamento

$2,2\cdot B<F_C<3\cdot B$

Inoltre, per rendere il filtro realizzabile, si introducono dei termini di ritardo, in modo tale che il filtro sia casuale; questo significa che il filtro avrà una fase lineare a pendenza non nulla (in banda utile).

È importante, in fase di progettazione, considerare il fatto che avere una frequenza di campionamento elevata ha un costo, in termini di numero di campioni da trasmettere e memorizzare, elettronica necessaria per il campionamento ecc.

Nel mondo reale, nessun filtro ha una risposta in frequenza costante (in modulo) all'interno della banda di interesse, così come nessun filtro ha risposta esattamente nulla nella zona di interdizione del filtro: il risultato di questa non idealità è una distorsione del segnale ricostruito che non può essere annullata, ma può almeno essere valutata e controllata, in modo tale da ridurre gli effetti della distorsione.

Torniamo al modello base dell'operazione di campionamento e ricostruzione;

File:Elaborazione segnali filtro campionamento ricostruzione ideale.png

Sample and hold

Il campionamento ideale non esiste, perché non esiste un oggetto in grado di generare la funzione $\delta$; quello che accade nella realtà è che l'elettronica è in grado di simulare un rettangolo stretto a piacere, ma la lunghezza non sarà mai nulla; inoltre, assieme all'operazione di campionamento viene fatta un'opearazione di quantizzazione, necessaria per esprimere le grandezze con un numero finito di bit.

Il campionamento con tenuta, o campionamento sample and hold, è un approccio che si può utilizzare per creare un blocco di conversione A/D (o ADC, Analogic to Digital Converter); quello che accade con un campionatore S&H è che viene estratto il valore della funzione $x(t)$ all'istante di campionamento, e viene mantenuto per un tempo lungo $T_C$, dopo il quale verrà preso un nuovo campione; di conseguenza, la funzione $x_c(t)$ assume l'aspetto di una funzione a gradini, non di una funzione impulsiva, dove si ha

$x_c(t)=\sum x(n\cdot T_C)rect\left(\frac{t-\frac{T_C}{2}-n\cdot T_C}{T_C}\right)$

File:Elaborazione segnali sample and hold funzione x c t .png

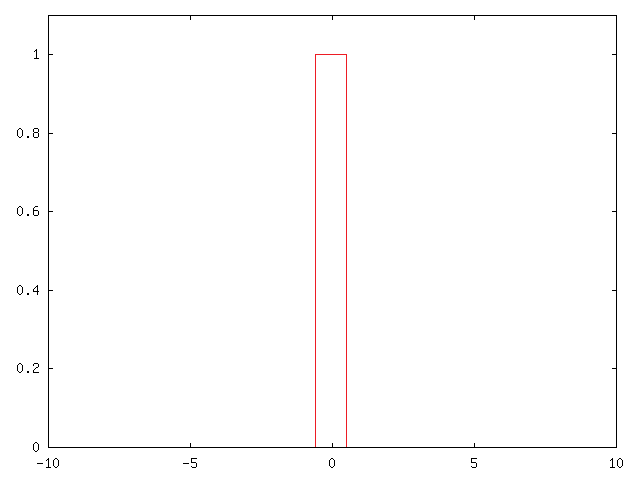
Con il campionatore S&H, l'impulso elementare $\delta$ è sostituito con un rettangolo di ampiezza $x(n\cdot T_C)$ e di durata $T_C$,

$\begin{array}{cc}{x}_{c,SH}(t)& =\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}x(k\cdot T_C)rect\left(\frac{t-\frac{T_C}{2}-n\cdot T_C}{T_C}\right)\\ & =x_c(t)*rect\left(\frac{t-\frac{T_C}{2}}{T_C}\right)*\delta (t-k\cdot T_C)\end{array}$

Trasformando, si ha

$h_{SH}(t)=rect\left(\frac{t-\frac{T_C}{2}}{T_C}\right)\leftrightarrow H_{SH}(f)=T_C\cdot sinc(f\cdot T_C)\cdot e^{-j2\pi f{T}_C/2}$

Si ottiene il seguente schema:

File:Elaborazione segnali sample and hold cascata sistema.png

dove si ha

$H_{SH}(f)\cdot H_{r,SH}(f)=H_r(f)$

La risposta all'impulso $h_{SH}(t)$ è la seguente:

File:Elaborazione segnali risposta tempo sample and hold.png

che è una funzione rettangolo, centrata in $\frac{T_C}{2}$ e di durata $T_C$; questo ritardo è dovuto alla necessità di avere dei filtri casuali, necessari per la realizzabilità fisica del filtro. Questa stessa funzione sarà usata, come vedremo più avanti, anche per ricostruire il segnale a partire dai campioni numerici: è detta ricostruttore, ed è l'interpolatore più semplice che si possa pensare.

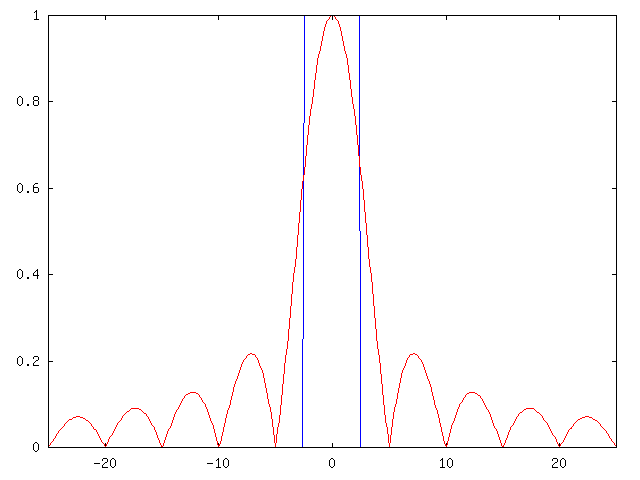
Il modulo della risposta all'impulso di questo filtro è la seguente:

In rosso vediamo il modulo che abbiamo ottenuto, mentre in blu vediamo il modulo che dovrebbe avere l'interpolatore ideale. L'espressione analitica del modulo della risposta all'impulso di questo interpolatore è

$|H_I(f)|=T_C\cdot |sinc(f\cdot T_C)|$

dove

$F_C=5$

Come si può vedere anche dal grafico, questo tipo di interpolatore introduce distorsione sia in banda utile che in banda fermata: il primo lobo del sinc va a zero negli istanti $F_C$ e $-F_C$, mentre l'interpolatore ideale va a zero per le frequenze $\frac{F_C}{2}$ e $-\frac{F_C}{2}$. I lobi successivi del sinc introducono delle componenti spettrali residue, provenienti dalle repliche del campionamento, che in origine non esistevano.

Per poter ovviare all'errore introdotto dal campionatore $h_{SH}(t)$ è necessario andare a modificare la risposta in frequenza dell'interpolatore, che da ideale diventa nella forma

$H_{r,SH}(f)=\frac{1}{sinc(f\cdot T_C)}rect\left(\frac{f}{F_C}\right)$

In questo modo, con il filtro ricostruttore si va ad uccidere la componente frequenziale residua che era rimasta in banda fermata, ed in più si amplifica il segnale in banda passate, di una quantità tale da compensare la caduta del sinc.

Filtro mantenitore

Il filtro manteritore, o Zero Order Hold, ZOH, è il filtro rettangolare che abbiamo visto per il campionatore S&H, ma usato per la ricostruzione del segnale invece che per il suo campionamento.

Calcoliamo l'errore che si commette usando un ricostruttore ZOH, considerando $x(t)$ come un segnale di energia; definiamo l'errore di interpolazione

$e_0(t)=x(t)-x_{r,ZOH}(t)$

e calcoliamo la potenza dell'errore di quantizzazione, che è

$\begin{array}{c}{W}_{e_0}=\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}|e_0(t){|}^{2}dt\\ & =\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}|E_0(f){|}^{2}df\\ & =\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}|X(f)-X_C(f)\cdot H_{ZOH}(f){|}^{2}df\end{array}$

Filtro di interpolazione lineare

Definiamo l'impulso triangolare $tri(t/T)$ come

$tri\left(\frac{t}{T}\right)=\{\begin{array}{cc}1-\frac{|t|}{T}& |t|\le T\\ 0& \text{altrove}\end{array}$

Da qui, definiamo l'interpolatore lineare come

$h_{LIN}(t)=tri\left(\frac{t-T_C}{T_C}\right)\leftrightarrow H_{LIN}(f)=T_C\cdot {(sinc(f\cdot T_C))}^2\cdot e^{-j2\pi f\cdot T_C}$

File:Elaborazione segnali filtro mantenitore impulso base.png

Anche in questo caso, l'impulso deve essere casuale, quindi è necessario introdurre un ritardo di un campione. Trasformando, il modulo della risposta in frequenza è

File:Elaborazione segnali filtro mantenitore impulso base modulo trasformata.png