Le Funzioni Circolari (superiori)

Nel riferimento cartesiano ortogonale è assegnato il vettore $\overrightarrow{u}$ di modulo unitario $(\left|\overrightarrow{u}\right|=1)$, applicato nell’origine del riferimento e con direzione e verso coincidenti con quelle dell’asse $x$. Il suo estremo libero è il punto $B(1;0)$.

Funzioni circolari

Facciamo ruotare $\overrightarrow{u}$ intorno all’origine in senso antiorario finché torna ad occupare la posizione iniziale, cioè quando ha compiuto una rotazione di $360\text{°}$. Muovendosi con continuità, l’estremo $B$ descrive la circonferenza con centro nell’origine, quella tratteggiata nella figura a fianco; le componenti del vettore cambiano con continuità e dipendono dall’angolo che, per ogni posizione, il vettore stesso forma con l’asse delle $x$. Ad esempio, quando $\overrightarrow{u}$ ha descritto nella rotazione un angolo di $90\text{°}$, l’estremo $B$ si trova in $B_1(0;1)$; quando $\overrightarrow{u}$ ha descritto nella rotazione un angolo di $180\text{°}$, l’estremo $B$ si trova in $B_2(-1;0)$; quando $\overrightarrow{u}$ ha descritto nella rotazione un angolo di $270\text{°}$, l’estremo $B$ si trova in $B_3(0;-1)$; e dopo una rotazione completa ($360\text{°}$) torna a coincidere con la posizione iniziale $B_4\equiv B(1;0)$.

DEFINIZIONE 1. La componente orizzontale $u_x$ del vettore unitario inclinato dell’angolo $\alpha$ rispetto all’asse $x$, si chiama coseno dell’angolo $\alpha$, in simboli $u_x=\cos (\alpha )$. Chiamiamo seno dell’angolo $\alpha$ la componente verticale $u_y$ del vettore unitario inclinato dell’angolo $\alpha$ rispetto all’asse $x$, in simboli $u_y=\sin (\alpha )$. Scriviamo $\overrightarrow{u}=(\cos (\alpha );\sin (\alpha ))$ o anche $B(\cos (\alpha );\sin (\alpha ))$.

Confrontando questa definizione con quanto descritto sopra possiamo innanzitutto affermare che seno e coseno di un angolo sono numeri reali positivi, negativi o nulli a seconda dell’angolo formato dal vettore e quindi della posizione del punto $B$ sulla circonferenza:

• se $\alpha =0\text{°}\Rightarrow B(1;0)\Rightarrow \overrightarrow{u}=(\cos (0\text{°});\sin (0\text{°}))\Rightarrow \cos (0\text{°})=1$ e $\sin (0\text{°})=0$;
• se $\alpha =90\text{°}\Rightarrow B(0;1)\Rightarrow \overrightarrow{u}=(\cos (90\text{°});\sin (90\text{°}))\Rightarrow \cos (90\text{°})=0$ e $\sin (90\text{°})=1$;
• se $\alpha =180\text{°}\Rightarrow B(-1;0)\Rightarrow \overrightarrow{u}=(\cos (180\text{°});\sin (180\text{°}))\Rightarrow \cos (180\text{°})=-1$ e $\sin (180\text{°})=0$;
• se $\alpha =270\text{°}\Rightarrow B(0;-1)\Rightarrow \overrightarrow{u}=(\cos (270\text{°});\sin (270\text{°}))\Rightarrow \cos (270\text{°})=0$ e $\sin (270\text{°})=-1$;
• se $\alpha =360\text{°}\Rightarrow B(1;0)\Rightarrow \overrightarrow{u}=(\cos (360\text{°})$;$\sin (360\text{°}))\Rightarrow \cos (360\text{°})=1$ e $\sin (360\text{°})=0$.

Per alcuni valori intermedi dell’angolo è possibile calcolare i relativi valori di seno e coseno usando metodi geometrici, per altri valori si può far uso della calcolatrice scientifica. Comunque, dai risultati sopra ottenuti, soprattutto riguardando la figura, possiamo affermare che qualunque sia l’angolo $\alpha$ sono sempre verificate le disuguaglianze: $-1\le \sin (\alpha )\le 1$ e $-1\le \cos (\alpha )\le 1$.

Ci proponiamo ora di tracciare il grafico della funzione $y=\sin (x)$. A questo scopo fermiamo la rotazione del vettore unitario ogni $30\text{°}$ (completate il disegno) e segniamo sulla circonferenza i punti $B_0$, $B_1$, $B_2$, ecc.

Funzioni circolari

Accanto alla rotazione del vettore unitario abbiamo tracciato un riferimento cartesiano dove sull’asse $x$ riportiamo le misure in gradi degli angoli descritti dal vettore unitario e sull’asse $y$ i valori assunti da $\sin (x)$, cioè dall’ordinata dell’estremo libero del vettore unitario che ruota in senso antiorario.

Per ogni angolo $x$ descritto riporteremo nel riferimento cartesiano $\sin (x)$. Il punto $B_0$ ha ordinata nulla dunque il primo punto che dobbiamo segnare nel riferimento cartesiano per costruire il grafico di $y=\sin (x)$ è l’origine; per segnare il punto di coordinate $P_1(30\text{°}$; $\sin (30\text{°}))$, da $B_1$ tracciamo la parallela all’asse $x$ fino ad incontrare la parallela all’asse $y$ tracciata da $30\text{°}$. Proseguite in questo modo per tutti gli altri punti $B_i$ della circonferenza per determinare i rispettivi punti $P_i$. Unendo i punti $P_i$ trovati si ha il grafico della funzione $y=\sin (x)$.

Noi l’abbiamo tracciato con GeoGebra. Notiamo che il valore massimo $1$ si ha per l’angolo di $90\text{°}$ mentre il minimo $-1$ si ha per l’angolo di $270\text{°}$. Se il vettore unitario dopo un giro completo ricominciasse nuovamente a ruotare in senso antiorario (positivo), descrivendo angoli maggiori di $360\text{°}$, il grafico si ripeterebbe identico al tratto compreso tra $0\text{°}$ e $360\text{°}$. Per questo motivo diciamo che la funzione $y=\sin (x)$ ha un andamento periodico.

La funzione seno

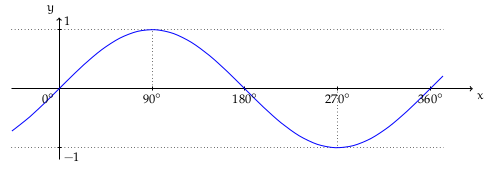
Abbiamo tracciato anche il grafico della funzione $y=\cos (x)$; sfruttando quanto fatto all’inizio del paragrafo; lasciamo al lettore di segnare sul grafico i valori dell’angolo per cui il coseno è nullo, il valore per cui il coseno assume il valore minimo $-1$, il punto del grafico di ascissa $=360\text{°}$. Per lo stesso discorso fatto sopra possiamo dire che la funzione $y=\cos (x)$ ha un andamento periodico.

La funzione coseno