Rette e Piani nello spazio

Rette e Piani nello spazio

Un piano nello spazio (quindi in 3 dimensioni) è l'insieme di tutti quei punti individuati dalla combinazione lineare di 2 vettori indipendenti aventi entrambi l'origine in un punto P.

Un esempio è il piano qui sotto.

Equazione cartesiana di un piano $\pi$ nello spazio

L'equazione cartesiana di un piano (che chiameremo $\pi$) si ricava in maniera simile all'equazione (cartesiana) della retta.

Sia $v=(a,b,c)$ un vettore applicato di ${ℝ}^3$ ortogonale al piano e $P_0=(x_0,y_0,z_0)$ un punto appartenente a $\pi$. Ogni punto di $\pi$ dovrà anch'esso essere perpendicolare a v, perciò anche qui ogni $P\cdot v-P_0\cdot v$ dovrà essere zero.

Abbiamo quindi che un punto P appartiene al piano $\pi$ se e solo se

$(P-P_0)\cdot v=0\iff (x-x_0,y-y_0,z-z_0)\cdot (a,b,c)=0\iff a(x-x_0)+b(y-y_0)+c(z-z_0)=0\iff$

$\iff ax+by+cz+(-a{x}_0-b{y}_0-c{z}_0)=0⟹ax+by+cz+d=0$

è l'equazione cartesiana del piano $\pi$.

Parallelismo, coincidenza e ortogonalità di piani

Siano :$\{\begin{array}{c}\pi :ax+by+cz+d=0\\ {\pi }^{\prime }:a^{\prime }x+b^{\prime }y+c^{\prime }z+d^{\prime }=0\end{array}$ due piani nello spazio rispettivamente ortogonali ai vettori $v=(a,b,c),v^{\prime }=(a^{\prime },b^{\prime },c^{\prime })\in {ℝ}^3$. Essi sono paralleli (cioè non si intersecano in nessun punto) se e solo se

$\mathrm{\exists }k\in ℝ\setminus \{0\}:v^{\prime }=kv\iff \{\begin{array}{c}{a}^{\prime }=ka\\ b^{\prime }=kb\\ c^{\prime }=kc\end{array}$

Un esempio di piani paralleli molto semplice che aiuta anche a capire quanto detto sopra è illustrato nella seguente figura;

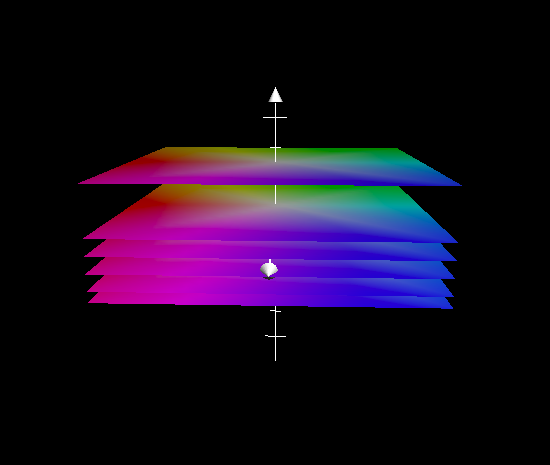
Se consideriamo come vettore v di ogni piano un vettore che sta sull'asse z (quello verticale), allora si vede chiaramente che ogni $kz$ genera un piano uguale agli altri, ma di "livello" diverso, in totale accordo con quanto detto sopra.

Se ad essere proporzionali non sono solo i vettori v ma anche i termini noti d, allora i piani sono coincidenti, cioè le varie equazioni descrivono lo stesso piano. Infatti:

$\{\begin{array}{c}ax+by+cz+d=0\\ a^{\prime }x+b^{\prime }y+c^{\prime }z+d^{\prime }=k(ax+by+cz+d)\end{array}\Rightarrow a^{\prime }x+b^{\prime }y+c^{\prime }z+d^{\prime }=k(0)=0$

L'equazione in forma implicita aiuta ulteriormente a capire questo concetto;

$z=ax+by+d\iff kz=k(ax+by+d)\iff z=\frac{k}{k}(ax+by+d)\iff z=ax+by+d$

Infine, l'ortogonalità di due piani $\pi$ e ${\pi }^{\prime }$ è verificata se e solo se sono ortogonali i vettori v e v' , cioè:

$v\cdot v^{\prime }=0\iff a{a}^{\prime }+b{b}^{\prime }+c{c}^{\prime }=0$

Piano per tre punti non allineati

Siano $P_0,P_1,P_2$ punti distinti dello spazio. Essi sono allineati se e solo se:

$P_1-P_0//P_2-P_0\iff \mathrm{r}\mathrm{g}\left(\begin{array}{cc}{x}_1-x_0& x_2-x_0\\ y_1-y_0& y_2-y_0\\ z_1-z_0& z_2-z_0\end{array}\right)<2$. Infatti 3 punti sono allineati se i vettori $P_1-P_0$ e $P_2-P_0$ sono paralleli e quindi se i vettori sono linearmente dipendenti.

Se $v_1=P_1-P_0,v_2=P_2-P_0$, per trovare l'equazione di un piano possiamo trovare un vettore ortogonale al piano generato da $v_1,v_2$ facendone il prodotto vettoriale ed ottenendo quindi un vettore ortogonale al piano. Sia $v=P-P_0$, allora

$v\cdot (v_1\wedge v_2)=0$

è l'equazione del piano cercato. Sviluppando i calcoli in termini di componenti si trova che l'equazione è data da

$\det \left(\begin{array}{ccc}x-x_0& y-y_0& z-z_0\\ x_1-x_0& y_1-y_0& z_1-z_0\\ x_2-x_0& y_2-y_0& z_2-z_0\end{array}\right)=0$

Rette nello spazio

Due rette $r_1,r_2$ si dicono parallele se hanno vettori direttori $u_1,u_2$ paralleli, incidenti se si incontrano in un punto, coincidenti se sono la stessa retta e sghembe se non sono né parallele né incidenti.

Le due rette sono parallele (o in particolare coincidenti) se e solo se i vettori direttori linearmente dipendenti, cioè se

$\mathrm{r}\mathrm{g}\left(\begin{array}{cc}{u}_1& u_2\end{array}\right)=1$.

Le due rette si intersecano in un punto $P$ quando è possibile scriverlo come elemento di $r_1$ e elemento di $r_2$, cioè $P_0+t{u}_1=P_1+s{u}_2$ ammette soluzione, in altri termini

$\mathrm{r}\mathrm{g}\left(\begin{array}{cc}{u}_1& u_2\end{array}\right)=\mathrm{r}\mathrm{g}\left(\begin{array}{ccc}{u}_1& u_2& P_0-P_1\end{array}\right)$

Se $\mathrm{r}\mathrm{g}\left(\begin{array}{cc}{u}_1& u_2\end{array}\right)=\mathrm{r}\mathrm{g}\left(\begin{array}{ccc}{u}_1& u_2& P_0-P_1\end{array}\right)=1$, il sistema ammette infinite soluzioni, cioè una "retta" di punti di intersezione. Quindi $r_1$ ed $r_2$ sono coincidenti.