Classificazione dei quadrilateri (scuola media)

Template:Risorsa In geometria il Template:Vk è un poligono con quattro Template:Vk, e quindi quattro Template:Vk e quattro Template:Vk, e due Template:Vk. Il quadrilatero è il poligono con il minor numero di lati nel quale si possono tracciare Template:Vk.

Video per chi non ama leggere: i quadrilateriTemplate:YouTube

I Template:Vk possono essere suddivisi a secondo delle relazioni tra i Template:Vk, tra gli Template:Vk e per le caratteristiche delle loro Template:Vk.

Classificazione dei quadrilateri attraverso i lati e le diagonali

Elementi nel quadrilatero

Quadrilateral elements

Gli elementi di un quadrilatero sono:

• i vertici $A,B,CeD$ (sono punti)
• i lati $AB,BC,CD,DA$ (sono segmenti)
• gli angoli interni $\hat{A},\hat{B},\hat{C},\hat{D}$, nella figura è evidenziato il solo angolo interno $\widehat{DAB}$
• gli angoli esterni che sono formati dal prolungamento di un lato e dal lato consecutivo, in figura è evidenziato solo l'angolo formato dal prolungamento del lato $DA$ con il lato $AB$
• le diagonali $ACeBD$

Nel quadrilatero:

• i lati $AB$ e $BC$ sono consecutivi
• i lati $AB$ e $BC$ sono adiacenti all'angolo $\hat{B}$
• i lati $AB$ e $CD$ sono opposti
• gli angoli $\hat{A}$ e $\hat{B}$ sono adiacenti al lato $AB$
• gli angoli $\hat{A}$ e $\hat{C}$ sono opposti
• i vertici $A$ e $B$ sono consecutivi
• le diagonali sono segmenti che uniscono vertici non consecutivi

osservando la figura si estendono queste definizioni a tutti gli altri elementi. Template:-

Esercizi per imparare gli elementi del quadrilatero

Quadrilateral elements

Facendo riferimento alla figura rispondi alle domande <quiz> {I lati $AD$ e $BC$ sono... |type="()"} -adiacenti +opposti -consecutivi

{Gli angoli $\hat{C}$ e $\hat{B}$ sono adiacenti al lato |type="()"} + $BC$ - $AB$ - $AC$

{I lati $CD$ e $DA$ sono... |type="()"} -adiacenti -opposti +consecutivi

{I vertici $C$ e $B$ sono... |type="()"} -adiacenti -opposti +consecutivi

{Gli angoli $\hat{B}$ e $\hat{D}$ sono... |type="()"} +opposti -consecutivi -adiacenti

</quiz> Template:-

Quadrilateri convessi

Somma angoli interni

La somma degli angoli interni di un quadrilatero convesso si può facilmente dedurre dal fatto che una diagonale lo taglia a metà dividendolo in due triangoli cosa che permette di calcolare la somma degli angoli interni come doppio rispetto a quella di un triangolo:

$S=2\cdot 180^{\circ }=360^{\circ }$

Diagonaaldriehoek2

cosa che corrisponde anche all'applicazione della formula generale

$S=(n-2)\cdot 180^{\circ }$

$S=2\cdot 180^{\circ }=360^{\circ }$

e così il quadrilatero regolare, il quadrato, avrà gli angoli interni che misurano

$S=\frac{2\cdot 180^{\circ }}{4}=\frac{360^{\circ }}{4}=90^{\circ }$

Numero delle diagonali

Anche il numero delle diagonali in un quadrilatero è facilmente ricavabile dall'osservazione, ed anche in questo caso l'osservazione viene confermata dalla teoria. Anche per calcolare il numero delle diagonali si può applicare la formula

$N_d=\frac{n\cdot (n-3)}{2}$

che per un quadrilatero diventa

$N_d=\frac{4}{2}=2$

Quadrilateri inscritti

Un poligono si può inscrivere in una circonferenza se tutti gli assi dei suoi lati si incontrano in un punto. Per i quadrilateri è possibile individuare un'altra condizione.

Quadrilatero inscritto

Tutti i triangoli con base un lato e vertici il circocentro sono isosceli, infatti i lati obliqui sono dei raggi della circonferenza. Gli angoli alla base di questi triangoli sono uguali e sommando gli angoli consecutivi si ottiene che gli angoli opposti del quadrilatero sono supplementari.

Quadrilateri circoscritti

Con una proprietà analoga dovuta alle tangenti che corrispondono ai lati otteniamo che in un quadrilatero circoscritto sono uguali le somme dei lati opposti.

Quadrilatero circoscritto

Classificazione

Possiamo procedere in due modi nella classificazione dei quadrilateri partendo dalla semplice caratteristica generica di avere 4 lati e aggiungendo man mano le proprietà che definiscono i diversi sottoinsiemi oppure partendo dal quadrilatero regolare il quadrato e levando mano a mano le proprietà che lo caratterizzano.

Dal quadrato ai quadrilateri

Il quadrato

Regular polygon 4 annotated

Il Template:Vk è probabilmente il poligono che viene studiato per primo nella carriera scolastica di uno studente. Il quaderno a quadretti favorisce il disegno di questo particolare quadrilatero.

Il quadrato ha molte proprietà:

• ha quattro lati uguali
• ha quattro angoli uguali

il quadrato è un poligono regolare per queste due prime proprietà

• ha due diagonali uguali e perpendicolari che si tagliano a metà

queste proprietà delle diagonali si possono usare per disegnare quadrati di grandi dimensioni

• è circoscrivibile e inscrittibile in una circonferenza

infatti il quadrato ha angoli opposti supplementari e sono uguali le somme di lati opposti

Straight Square Inscribed in a Circle 240px

Esercizi per imparare le proprietà del quadrato

<quiz> {Il lati del quadrato sono |type="()"} -uguali a due a due +tutti uguali -uguali solo gli opposti

{Gli angoli del quadrato sono tutti e quattro di |type="()"} - 60° - 45° + 90°

{LA somma di due angoli opposti del quadrato fa |type="()"} -360° -90° +180°

{Le diagonali del quadrato sono |type="()"} +perpendicolari -proporzionali -parallele

{Il quadrato rispetto ad una circonferenza è |type="()"} +circoscribile e inscrittibile -solo inscrittibile -solo circoscrivibile

</quiz> Template:-

Il rettangolo

Anche il rettangolo si disegna facilmente su un quaderno a quadretti

Rectangle 4x5

Le proprietà del rettangolo sono:

• ha quattro angoli uguali

ma non avendo i lati uguali il rettangolo non è un Template:Vk

• ha due diagonali uguali che si tagliano a metà

queste proprietà delle diagonali si possono usare per disegnare rettangoli di grandi dimensioni

• è inscrittibile in una circonferenza

ovviamente gli angoli opposti sono supplementari, infatti sono due retti, si può anche osservare che i vertici del rettangolo sono equidistanti dal punto di incontro delle diagonali,

• non è circoscrivibile ad una circonferenza

infatti non sono uguali le somme dei lati opposti

Krug opisan oko pravougaonika

Esercizi per imparare le proprietà del rettangolo

<quiz> {Il lati del rettangolo sono |type="()"} -tutti diversi -tutti uguali +uguali gli opposti

{Gli angoli del rettangoloo sono tutti uguali di |type="()"} - 60° - 45° + 90°

{La somma di due angoli opposti del rettangolo fa |type="()"} -360° -90° +180°

{Le diagonali del rettangolo sono |type="()"} +uguali ma non perpendicolari -uguali e perpendicolari -perpendicolari ma non uguali

{Il rettangolo rispetto ad una circonferenza è |type="()"} -circoscribile e inscrittibile +solo inscrittibile -solo circoscrivibile

</quiz> Template:-

Il rombo

Rhombus (polygon)

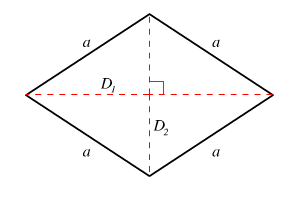
Le proprietà del rombo sono:

• ha quattro lati uguali

ma non avendo gli angoli uguali il rombo non è un Template:Vk

• ha due diagonali perpendicolari che si tagliano a metà

queste proprietà delle diagonali si possono usare per disegnare rombi di grandi dimensioni

• è circoscrivibile ad una circonferenza

le quattro bisettrici degli angoli si incontrano nel centro del rombo e sono uguali le somme dei lati opposti

• non è inscrittibile in una circonferenza

infatti gli angoli opposti non sono supplementari

Rombo 109

Esercizi per imparare le proprietà del rombo

<quiz> {Il lati del rombo sono |type="()"} -tutti diversi +tutti uguali -uguali gli opposti

{Gli angoli del rombo sono |type="()"} - tutti diversi - tutti uguali di 45° + uguali gli opposti

{Le bisettrici dei quattro angoli coincidono con |type="()"} -i lati -le altezze +le diagonali

{Le diagonali del rombo sono |type="()"} -uguali ma non perpendicolari -uguali e perpendicolari +perpendicolari ma non uguali

{Il rombo rispetto ad una circonferenza è |type="()"} -circoscribile e inscrittibile -solo inscrittibile +solo circoscrivibile

</quiz> Template:-

Il parallelogramma (romboide)

Parallelogramma

Il Template:Vk, anche detto romboide deve il suo nome al fatto di avere i lati opposti paralleli.

Le proprietà del parallelogramma quindi sono:

• lati opposti paralleli
• lati opposti uguali
• angoli opposti uguali
• angoli adiacenti allo stesso lato supplementari
• diagonali che si tagliano a metà, ma non sono uguali

Esercizi per imparare le proprietà del parallelogramma

<quiz> {Il lati del parallelogramma sono |type="()"} +paralleli a due a due -tutti uguali -adiacenti uguali

{Il parallelogramma ha |type="()"} - gli angoli adiacenti uguali - quattro angoli uguali + gli angoli opposti uguali

{Gli angoli adiacenti del parallelogramma sono |type="()"} -uguali -complementari +supplementari

{Le diagonali del parallelogramma |type="()"} +si tagliano a metà -sono uguali -sono parallele

{Il parallelogramma rispetto ad una circonferenza è |type="()"} +né circoscribile né inscrittibile -solo inscrittibile -solo circoscrivibile

</quiz> Template:-

Il trapezio

Trapezio

Trapezoid

Il Template:Vk è il quadrilatero che aggiunge alla proprietà di avere quattro lati quella di avere due di essi paralleli.

Grazie a questa proprietà si possono così distinguere gli elementi del trapezio:

• la base maggiore, il lato maggiore dei due lati paralleli
• la base minore, ovviamente, il lato più corto dei due lati paralleli
• i lati obliqui
• la distanza tra le due basi parallele è l'altezza del trapezio

Le proprietà del Template:Vk sono:

• due lati paralleli
• angoli adiacenti ai lati obliqui supplementari

questa seconda proprietà è una conseguenza della prima per le proprietà delle rette parallele tagliate da una trasversale,

I trapezi si possono classificare in tre diversi tipi:

• scaleni
• isosceli
• rettangoli

• 
  Il Template:Vk scaleno ha lati obliqui diversi e di conseguenza quattro angoli diversi.
• 
  Il Template:Vk isoscele ha i lati obliqui uguali e di conseguenza angoli adiacenti alla base maggiore uguali tra loro così come i due angoli adiacenti alla base minore.
• 
  Il Template:Vk rettangolo ha due angoli retti poichè ha uno dei due lati obliqui perpendicolare alle basi.
• 
  Il Template:Vk ottusangolo ha un angolo ottuso

Template:-

Trapezio e circonferenza

Isosceles trapezoid rotation

Il trapezio isoscele è sempre inscrittibile in una circonferenza infatti gli angoli opposti sono supplementari. Non lo sono il trapezio rettangolo e quello scaleno, gli angoli opposti non sono sicuramente supplementari, se lo fossero si ricadrebbe nel caso del trapezio isoscele e del rettangolo.

Tutti e tre i diversi tipi di trapezio possono però soddisfare la condizione per essere circoscritti, in alcuni casi quindi il trapezio isoscele è sia inscritto che circoscritto, circocentro e incentro non coincidono però a meno di non considerare il caso limite del quadrato.

• 
  Trapezio Circoscritto
• 
  Trapezio Rettangolo Circoscritto
• 
  Trapezio Isoscele Inscritto
• 
  Trapezio Isoscele Inscritto Circoscritto

Esercizi per imparare le proprietà del trapezio

<quiz> {Il trapezio ha solo |type="()"} -due lati uguali +due lati paralleli -due angoli uguali

{Gli angoli adiacenti ai lati obliqui sono |type="()"} - uguali + supplementari - paralleli

{Un trapezio rettangolo ha |type="()"} -un solo angolo retto -quattro angoli retti +due angoli retti

{Le diagonali del trapezio isoscele sono |type="()"} -perpendicolari +uguali -parallele

{La somma degli angoli interni del trapazio è |type="()"} +360° -180° -540°

</quiz> Template:--->

Dai quadrilateri al quadrato

Quadrilateri convessi

Tra tutti i quadrilateri il sottoinsieme che mostra di avere proprietà geometricamente significative è quello dei quadrilateri convessi.

Tabella riassuntiva

	...	...	..
...	...	...	...
...	...	...

Bibliografia

Contaci Zanichelli, autori: Clara Bertinetto, Arja Metiainen, Johannes Paasonen, Eija Voutilainen

Collegamenti esterni

w:Trapezio 4:1=