Funzioni derivabili e derivata di una funzione

Rapporto incrementale e definizione di derivata

Diamo prima la definizione di derivata di una funzione, poi discutiamone il significato. Template:Riquadro

In termini geometrici, il rapporto incrementale di una funzione è il coefficiente angolare della retta secante la funzione e passante per i punti di ascissa $x_0$ e $x$. Vediamone un esempio grafico intuitivo.

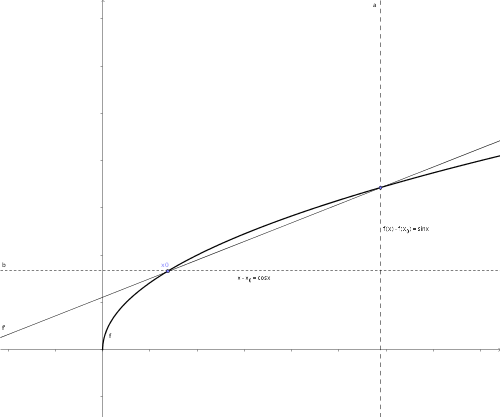
Dalla geometria analitica sappiamo inoltre che il coefficiente angolare di una retta è uguale alla tangente dell'angolo che si viene a formare tra essa e una qualsiasi retta parallela all'asse delle ascisse.

Essendo $f(x)-f(x_0)=\sin \beta$ e $x-x_0=\cos \beta$, la tangente $\frac{\sin \beta }{\cos \beta }$, cioè il coefficiente angolare della nostra retta è $\frac{f(x)-f(x_0)}{x-x_0}$ che è proprio il rapporto incrementale!

Osservazione

Dimostrazione

Supponiamo che $f$ sia continua. Allora $f(x)-f(x_0)$ tende a 0 per $x$ che tende a $x_0$. Allora

$f(x)-f(x_0)=\frac{f(x)-f(x_0)}{x-x_0}(x-x_0)$

il rapporto incrementale tende a $f^{\prime }(x_0)$ e $x-x_0$ tende a $0$ per $x\to x_0$. Dunque:

$\underset{x\to x_0}{\lim }\frac{f(x)-f(x_0)}{x-x_0}(x-x_0)=0$ anch'esso, come volevamo dimostrare.

$◻$

È interessante notare esplicitamente che l'implicazione inversa non vale in generale. Facciamo un controesempio; $f:ℝ\to ℝ,f(x)=\mid x\mid$. La funzione valore assoluto è certamente continua (addirittura è continua in ogni punto del suo dominio, dunque anche in $x_0$, tuttavia $f$ non è derivabile nel punto $x_0=0$.

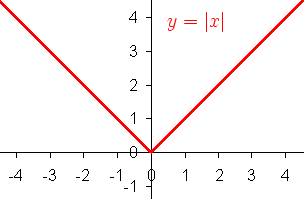
Infatti

$\underset{x\to 0}{\lim }\frac{|x|}{x}=\{\begin{array}{cc}1& \text{per}x\to 0^{+}\\ \\ -1& \text{per}x\to 0^{-}\end{array}$.

I due limiti sono diversi, dunque non esiste il limite del rapporto incrementale e la funzione non è derivabile.

Esempi di funzioni derivabili

Vediamo ora alcuni esempi di funzioni notevoli derivabili e ne calcoliamo poi la derivata. Prima un appunto di notazione. Template:Riquadro

1 - derivata di una potenza

$f:ℝ\to ℝ,f(x)=x^n,n\in \mathbb{N}$. Dimostriamo che $f^{\prime }(x)=n{x}^{n-1}$. Infatti, tenendo a mente che $a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}{b}^2+\dots +a{b}^{n-2}+b^{n-1}$) abbiamo:

$\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}\Rightarrow \underset{h\to 0}{\lim }\frac{(x+h{)}^n-x^n}{h}=$ $\underset{h\to 0}{\lim }\frac{((x+h)-x)((x+h{)}^{n-1}+(x+h{)}^{n-2}x+\dots +(x+h)x^{n-2}+x^{n-1})}{h}$

$\underset{h\to 0}{\lim }\frac{h((x+h{)}^{n-1}+(x+h{)}^{n-2}x+\dots +(x+h)x^{n-2}+x^{n-1})}{h}=$ $\underset{h\to 0}{\lim }((x+h{)}^{n-1}+(x+h{)}^{n-2}x+\dots +(x+h)x^{n-2}+x^{n-1})=$ $=\sum _{i=1}^n{x}^{n-1}=n{x}^{n-1}$

2 - derivata di $e^x$

Dimostriamo che la derivata di $f(x)=e^x$ è uguale a $f^{\prime }(x)=e^x$. Fissiamo $x\in ℝ$ e sfruttiamo la definizione di derivata intesa come limite del rapporto incrementale centrato in $x$:

$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}\Rightarrow \underset{h\to 0}{\lim }\frac{e^{x+h}-e^x}{h}=\underset{h\to 0}{\lim }{e}^x\frac{e^h-1}{h}$.

Quando $h\to 0$ si ha che:

• $e^x$ tende a $e^x$ perché tale fattore non dipende dalla variabile $h$;
• $\frac{e^h-1}{h}$ tende a 1 per via del limite notevole associato all'esponenziale;

pertanto il limite precedente è uguale a $e^x$. Concludiamo quindi che la derivata della funzione esponenziale $f(x)=e^x$ coincide con se stessa, ossia:

$f^{\prime }(x)=e^x$

che è quello che volevamo dimostrare.

3 - derivata di $\log x$

$\underset{x\to x_0}{\lim }\frac{\log x-\log x_0}{x-x_0}$. Scriviamo $\log x=y\iff e^y=x$ e $\log x_0=y_0\iff e^{y_0}=x_0$.

$\frac{y-y_0}{e^y-e^{y_0}}=\frac{1}{\frac{e^y-e^{y_0}}{y-y_0}}$. Abbiamo che $x\to x_0\Rightarrow \log x\to \log x_0\Rightarrow y\to y_0$ e dunque il denominatore tende a $D{e}^{y_0}=e_0^y=x_0$. Dunque $D\log x=\frac{1}{x}$.

4-Derivata delle funzioni circolari

Dimostriamo che $D\sin x=\cos x,\mathrm{\forall }x\in ℝ$ e $D\cos x=-\sin x,\mathrm{\forall }x\in ℝ$.

Premettiamo però un limite che non dimostreremo adesso ma che si rivela molto utile: $\underset{h\to 0}{\lim }\frac{\sin h}{h}=1$.

Ora: $\underset{h\to 0}{\lim }\frac{1-\cos h}{h^2}=\underset{h\to 0}{\lim }\frac{(1-\cos h)(1+\cos h)}{h^2(1+\cos h)}=$ $\underset{h\to 0}{\lim }\frac{1-{\cos }^{2}h}{h^2(1+\cos h)}=\underset{h\to 0}{\lim }{\left(\frac{\sin h}{h}\right)}^2\frac{1}{1+\cos h}=\frac{1}{2}$

Adesso procediamo con la dimostrazione della derivata di $\sin x$.

$\underset{h\to 0}{\lim }\frac{\sin (x+h)-\sin x}{h}=\underset{h\to 0}{\lim }\frac{\sin x\cos h+\sin h\cos x-\sin x}{h}=$ $\underset{h\to 0}{\lim }(\sin x\frac{\cos h-1}{h}+\cos x\frac{\sin h}{h})$.

$\sin x\frac{\cos h-1}{h}$ tende a 0 mentre $\cos x\frac{\sin h}{h}$ tende a $\cos x\cdot 1=\cos x$. Dunque ecco dimostrata la derivata notevole del seno.

Analoghe dimostrazioni provano la derivata delle altre funzioni circolari e sono lasciate per esercizio.

Vediamo ora un'ultima osservazione estremamente importante.

Osservazione

Esempi

Consideriamo ad esempio la funzione $f(x)=\sin (x)$ e $x_0=0$. Per applicare la relazione

$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\omega (x)(x-x_0)$

abbiamo la necessità di valutare la derivata prima di $f(x)=\sin (x)$ nel punto $x_0=0$. Nel paragrafo relativo alle derivate delle funzioni circolari abbiamo dimostrato che $f^{\prime }(x)=\cos (x)$ di conseguenza $f^{\prime }(0)=\cos (0)=1$. Ora disponiamo di tutte le informazioni necessarie per utilizzare la relazione

$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\omega (x)(x-x_0)$

che diventa

$\sin (x)=\sin (0)+\cos (0)(x-0)+\omega (x)(x-0)$

vale a dire

$\sin (x)=x+\omega (x)\cdot x$

Scriviamo la formula in favore di $\omega (x)$:

$\omega (x)=\frac{\sin (x)-x}{x}\text{per }x\ne 0$

e infine ne calcoliamo il limite per $x$ che tende a $x_0$

$\underset{x\to 0}{\lim }\omega (x)=\underset{x\to 0}{\lim }\frac{\sin (x)-x}{x}=\underset{x\to 0}{\lim }(\frac{\sin (x)}{x}-\frac{x}{x})=$

$=\underset{x\to 0}{\lim }(\frac{\sin (x)}{x}-1)=0$

Il limite è zero perché $\frac{\sin (x)}{x}\to 1$ per $x\to 0$, in virtù del limite notevole del seno.