Le cortine trainate e le loro caratteristiche acustiche

Template:Risorsa

I sottomarini, per la scoperta dei bersagli attivi molto lontani, a volte, utilizzano basi acustiche di notevole lunghezza, rilasciate e trainate come code del battello stesso; queste basi sono identificate con il termine di "Cortine trainate".

In figura 1 è mostrato, con un semplice disegno non in scala, un sommergibile con la cortina estesa.

Il disegno mostra come la cortina sia tenuta, tramite il cavo di traino, a notevole distanza dal battello per ridurre al massimo le interferenze acustiche del sottomarino sulla cortina stessa.

Sulle dimensioni e la struttura delle cortine trainate

La cortina trainata è formata da un lungo tubo di materiale plastico, trasparente al suono, all'interno del quale sono cablati numerosi elementi idrofonici, generalmente di tipo cilindrico, dotati di preamplificatori a basso rumore.

All'interno del sottomarino le cortine sono avvolte in speciali tamburi che oltre alla ottimale sistemazione volumetrica consentono il loro collegamento con un dedicato settore funzionale del sonar di bordo.

Generalmente il collegamento al sonar prevede tante connessioni separate quante sono le zone acusticamente sensibili della cortina ( possono essere per ciascun elemento idrofonico o per gruppi di elementi).

Una bella immagine di cortina trainata è mostrata in figura 2, diapositiva tratta da conferenza 5 Marzo 2014 presso Circolo Uff. MMI La Spezia, dalla quale si possono dedurre, di massima, dimensioni e struttura:

Le caratteristiche della cortina di figura 2, saranno assunte come base per l’esercizio di calcolo di questa lezione.

Le frequenza di lavoro delle cortine trainate

Grazie alla possibilità di realizzare cortine di notevoli lunghezze lo spettro delle frequenze di ricezione è collocabile nella parte inferiore del campo di lavoro dei sistemi di localizzazione subacquea.

Questa caratteristica consente portate di scoperta molto elevate dato che l'attenuazione del suono per assorbimento, a frequenze molto basse, è quasi irrilevante come mostra la curva di figura 3.

La curva è rappresentativa della funzione di Thorp riportata nella 1)

$1)$

che computa l'attenuazione in $dB/km$ in funzione di $fo$ ( frequenza media geometrica della banda ) espressa in $kHz.$

Il diagramma di figura 3 mostra come l'attenuazione per assorbimento decresca molto rapidamente con il decrescere della frequenza; un'idea si può avere supponendo di ricevere i segnali idrofonici in banda $100-500Hz$ , in tal caso la frequenza media geometrica è $fo=223Hz=0.223kHz$ che, secondo figura 3, porta ad un'attenuazione per assorbimento estremamente piccola: circa $0.004dB/km$ .

Il calcolo del guadagno di direttività delle cortine trainate

In linea di massima il guadagno di direttività di una cortina trainata ad $n$ sensori è stimabile con l'espressione:

$G=10\cdot lo{g}_{10}n$

valida se gli $n$ sensori sono disposti alla distanza di $\lambda /2$ l'uno dall'altro

dove $\lambda =1530/fo.$

Prendendo ad esempio i valori di frequenza riportati in figura 3) si ha:

$\lambda =1530/fo=1530/223=6.86me\lambda /2=3.43m$

Se la cortina ha una lunghezza di $100m$ il numero dei sensori sarà:

$n=100/3.43\approx 30$

ed infine il calcolo di $G$ :

$G=10\cdot lo{g}_{10}30\approx 15dB$

La curva di direttività di una cortina trainata

La curva di direttività di una cortina trainata può essere calcolata secondo l'algoritmo di Stenzel:

$R(\alpha )=\sqrt[]{(1/n)+(2/n^2)\cdot \sum _{m=1}^j\{(n-m)\cdot [\sin (m\cdot p\cdot x)/(m\cdot p\cdot x)]\cdot \cos [(p+2)\cdot m\cdot x]\}}$

Dove:

$n=$ numero degli idrofoni

$j=n-1$

$d=L/(n-1)$

$L=$ lunghezza della base in metri

$c=$ velocità del suono in $m/s$

$x=(\pi \cdot d\cdot f_1/c)\cdot \sin \alpha$

$f_1=$ frequenza inferiore della banda

$f_2=$ frequenza superiore della banda

$p=(f_2-f_1)/f_1$

Possiamo ora calcolare la curva di direttività nel piano orizzontale, al traverso, secondo $\alpha$ variabile di $+/-20$° ed in base ai dati visti in precedenza:

• $n=30$
• $L=100m$
• $d=3.45$
• $x=(3.14\cdot d\cdot f1/c)\sin \alpha$
• $f1=100Hz$
• $f2=500Hz$
• $p=4$

Il risultato del calcolo in funzione dell'angolo di puntamento è riportato nel grafico di figura 4 nel caso di sorgente acustica posta al traverso della cortina trainata:

La curva, tracciata in coordinate cartesiane, evidenzia una larghezza $\mathrm{\Delta }\alpha$ del lobo a $-3dB$ pari a circa $2.8$° .

Dato che in figura 4 l'intervallo delle ascisse copre un arco di soli $+/-20$° non si evidenzia il fatto fondamentale che la cortina trainata, non essendo schermata da nessuna parte, presenta, sul piano orizzontale, la stessa caratteristica di direttività per la direzione opposta, a $180$° rispetto a quella indicata in figura.

La rappresentazione della caratteristica di direttività nel piano orizzontale, tracciata in coordinate polari, vedi figura 5, consente la visione completa del diagramma mettendo in evidenza la contemporaneità dei due lobi contrapposti di $180$°

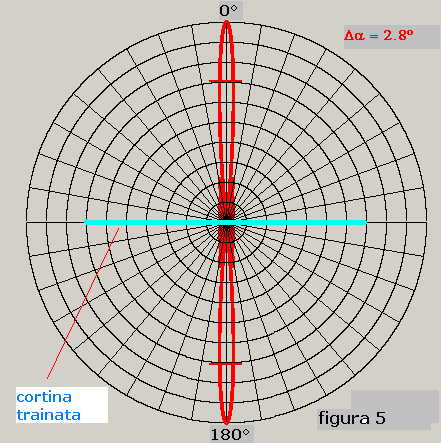
Come si vede dalla figura 5 la base idrofonica in esame presenta ambiguità di scoperta; infatti, una volta, individuato un bersaglio non era possibile stabilire se questo si trovasse sulla destra o sulla sinistra rispetto all'asse longitudinale della cortina.

Il problema è stato risolto impiegando, invece che singoli elementi sensibili, triplette di trasduttori disposti a stella; con una opportuna elaborazione dei segnali provenienti dalle triplette si ottiene l'abbattimento di uno dei lobi che crea ambiguità.

Portate di scoperta di una cortina trainata

E' indicativo dell'impiego di una cortina trainata il calcolo della portata di scoperta che, nei casi di propagazione normale, al di fuori dallo strato di mare nel quale il termoclino è piu penalizzante , può realizzare condizioni di scoperta eccellenti.

Con l'ausilio del calcolatore SONARMATH ( lezione 1^ della materia Sistemi di calcolo automatico per il sonar ), sia con i dati elaborati in precedenza, sia con nuove grandezze da stabilire, eseguiamo un calcolo di previsione di portata per la cortina trainata indicata al paragrafo 2) secondo le variabili :

• Scoperta con rivelatori in correlazione
• Costante di tempo d'integrazione $RC=1s$
• Assunta $Priv=90\mathrm{\%}ePfa=5\mathrm{\%}$ si ha $d=8.5$
• $f1=100Hz$
• $f2=500Hz$
• $fo=223Hz$
• $SL$; caccia a bassa velocità ( $v<10nodi$) e $fo=223Hz$ : $SL=130dB/\mu Pa/Hz$
• $NL$; per mare $SS=2$ e $fo=223Hz$ : $NL=72dB/\mu Pa/Hz$
• $DI$ in correlazione pari a $DI=G-3dB=15-3=12dB$
• propagazione sferico-cilindrica

Dal calcolo e dal grafico ottenuti con SONARMATH, mostrati in figura 6 risulta:

Portata $R=89km$ ; il dato è certamente al di sopra delle portate di scoperta ottenibili con basi idrofoniche montate sulle strutture del sottomarino nel caso che il bersaglio navigasse lentamente come nel caso trattato ($v<10nodi$).

Bibliografia

• R. J. Urick, Principles of underwater sound, 3ª ed., Mc Graw – Hill, 1968.

• H&B Stenzel, Leitfaden zur berechnung von schallvorgangenh, Berlino, Julius Springer, 1939.

• C. Del Turco, SONAR, Testo a cura dell'Accademia Navale di Livorno per i corsi di Abilit. Smg. AS/T, Agg. Prof. EA/AST 1992.

Siti di riferimento

https://www.ametek-ecp.com/resources/blog/2019/march/towed-array-sonar-uses-and-design-challenges

https://doi.org/10.1007/s40857-019-00157-2