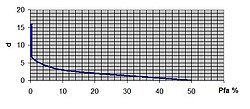
Probabilità di falso allarme nel sonar e distanza dal bersaglio

Presentazione video del sonar Fa1; Fa2; Fa3 = Falsi allarmi - S+n = segnale e disturbo

Con la dizione probabilità di falso allarme nel sonar e distanza dal bersaglio s'intende individuare un'area di studio che mostri come la probabilità di avere numerosi falsi allarmi, Fa1, Fa2, Fa3 ..., nella ricerca sonar di un bersaglio attivo s'incrementi con l'aumento della distanza del bersaglio stesso.

L'area di studio è imperniata su di un processo matematico che consente di valutare le incertezze della localizzazione in dipendenza dell'allontanamento del bersaglio da un punto a distanza stabilita.

Calcolo della probabilità di falso allarme Pfa. = f ( R )

Generalmente la percentuale di probabilità di falso allarme in un sonar, nel contesto del calcolo della portata, viene considerata come un valore unico assunto nelle computazioni in base alle necessità operative del momento.

Lo studio della variazione della percentuale di probabilità di falso allarme, in funzione della distanza del bersaglio vede, in vece, come varia tale percentuale secondo la relazione implicita: $Pfa.=f(R)$.

Dati di base

Il calcolo inizia con la determinazione di una portata di scoperta di riferimento per sistemi di sonar in correlazione; questa sarà la base di partenza di tutti gli sviluppi successivi che impiegano le funzioni sotto indicate, ciascuna con il proprio grafico ,necessario per la soluzione del problema stesso:

-$d=f(Pfa.)$: parametro probabilistico (curve ROC), con $Priv.=costante$ (Funzione A)

-$DT=f(d)$: differenziale di riconoscimento (Funzione B)

-$R=f(DT)$ : distanza del bersaglio (Funzione C)

dalle quali, infine, ricavare la funzione che risolve il problema posto:

$Pfa.=f(R)$: probabilità di falso allarme in funzione della distanza R (Funzione risolutiva)

Portata di scoperta di riferimento

Per risolvere il problema posto i computi iniziano con la determinazione della portata di scoperta di riferimento, $Rf$:

Nel caso di sonar passivo, con propagazione sferica, secondo le equazioni:

$\{\begin{array}{c}TL=60+20\cdot {\log }_{10}R+\alpha \cdot R\\ TL=SL+DI-NL-DT+10\cdot {\log }_{10}BW\end{array}$

La soluzione grafica del sistema trascendente si ottiene assumendo, ad esempio, le variabili:

-$SL=140dB/\mu Pa/Hz$

-$NL=58dB/\mu Pa/Hz$ -$\alpha =0.1dB/km$

-$DI=10dB$

-$DT=27.2dB$

-$BW=2250Hz$

-$RC=0.1s$

-$d=28(Priv.=60\mathrm{\%};Pfa.=0.0001\mathrm{\%})$

La soluzione in base alle variabili assunte è mostrata in figura :

Soluzione grafica sistema trascendente

Template:Clear in cui:

-la retta rossa rappresenta la prima equazione del sistema

-la curva blu rappresenta la seconda equazione del sistema

-l'ascissa del loro punto d'intersezione indica la portata calcolata:

$Rf=46km$

Da questa distanza di riferimento si considera l'allontanamento del bersaglio e il conseguente aumento della probabilità di falsi allarmi $Pfa=f(R)$ con la probabilità di rivelazione costante $Priv=60\mathrm{\%}$.

Procedura per il calcolo delle funzioni

Funzione A: d = f (Pfa.)

• 
  Porzione di curve ROC, retta rossa per Priv = 60 %
• 
  d = f( Pfa.) per Priv = 60 % costante

La funzione $d=f(Pfa.)$ per $Priv=60$% costante, dipendente dalle curve ROC, è calcolata per valori discreti impiegando una porzione di dette curve riportate nella figura di sinistra dalla quale si rilevano le coppie $def(Pfa.)$ che generano la curva a punti $d=f(Pfa.)$riportata nella figura di destra.

Funzione B : DT = f(d)

La funzione $DT=f(d)$, per $Priv.=60$% costante, dipendente dalla curva $d=f(Pfa.)$, è tracciata secondo l'equazione :

$DT=5\cdot lo{g}_{10}[(BW\cdot d)/(2\cdot RC)]$

nella quale le variabili sono le stesse impiegate nella seconda sottosezione per il calcolo di $Rf$; la funzione è mostrata in figura

DT = f( d )

Funzione C : R = f(DT)

La funzione trascendente $R=f(DT)$ per $Priv=60$% costante. si computa secondo l'algoritmo seguente::

$60+20\cdot {\log }_{10}R+\alpha \cdot R=SL+DI-NL-DT+10\cdot {\log }_{10}BW$

dipende dalla curva $DT=f(d)$ precedentemente tracciata.

In figura l'andamento di $R$ in funzione di $DT$ dove le variabili sono le stesse impiegate per il calcolo di $Rf$

R = f( DT )

Funzione risolutiva: Pfa. = f(R)

Con il calcolo per coppie di punti della funzione $Pfa.=f(R)$, per $Priv=60$% costante, si ottiene la soluzione del problema posto.

Calcolo della prima coppia di punti

I punti di $Pfa.=f(R)$ seguono le corrispondenze dei punti delle tre curve precedenti secondo la successione numerica nelle uguaglianze:

Assunto ad esempio $Pfa.=1\mathrm{\%}$

-da $d=f(Pfa.)$ si ha la coppia:

$Pfa.=1\mathrm{\%}$; $d=6$

-da $DT=f(d)$ si ha la coppia:

$d=6$ ; $DT=24dB$

-da $R=f(DT)$ si ha la coppia:

$DT=24dB$ ; $R=65km$

-di conseguenza varrà la coppia $Pfa.=f(R)$ :

$Pfa.=1\mathrm{\%}$; $R=65km$

Calcolo dell'insieme delle coppie di punti

Seguendo la procedura della sezione precedente per tutti i punti di $Pfa$ si determinano le coppie che generano la curva di figura:

Pfa. = f(R)

La curva mostra l'incremento della probabilità di falso allarme $Pfa$ , per $Priv.=60$% costante, con l'aumentare della distanza $R$; da $Rf=46km$ di riferimento, con $Pfa=.1\mathrm{\%}$ a $R=110km$ con $Pfa=50\mathrm{\%}.$

note

Annotazioni

Fonti

Bibliografia

• Robert J. Urick, Principles of underwater sound , Mc Graw – Hill|edizione=3ª, 1968

• Template:Cita libro

Collegamenti esterni

N° FASCI Selenia

Sonar FALCON

Schemi sonar FALCON

Testo discorsivo sul sonar

Testo tecnico sulla Correlazione