Lezione precedente: Minimizzazione degli stati di un automa

Introduzione

Dato che per definizione i linguaggi sono degli insiemi, è possibile applicare ad essi le operazioni insiemistiche (unione, intersezione, complementazione, differenza, ...). In questa lezione ci occuperemo di dimostrare che, quando le operazioni insiemistiche coinvolgono linguaggi regolari, il loro risultato sarà anch'esso un linguaggio regolare o, detto più brevemente, i linguaggi regolari sono chiusi rispetto alle operazioni insiemistiche che analizzeremo.

Prima di addentrarci nei dettagli delle dimostrazioni indagheremo il significato delle proprietà di chiusura per i linguaggi regolari, con l'obiettivo di capire quale sia il loro ruolo nell'ambito dell'informatica teorica. A questo scopo discutiamo un breve esempio: a partire dall'alfabeto $I = {0, 1}$ costruiamo due linguaggi regolari $L_{2}$ e $L_{3}$ . Gli elementi di questi insiemi sono stringhe che rappresentano numeri binari; nel caso di $L_{2}$ sono multipli di due, nel caso di $L_{3}$ sono multipli di 3. Per inciso, può essere un buon esercizio dimostrare che i due linguaggi sono effettivamente regolari (suggerimento: basta costruire un accettore a stati finiti in grado di riconoscerli).

L'insieme $L_{2} \cap L_{3}$ conterrà tutti i numeri che sono sia multipli di due sia multipli di 3, ossia tutti i multipli di 6; potremo scrivere $L_{6} = L_{2} \cap L_{3}$ . Possiamo interpretare questo risultato affermando che i linguaggi $L_{2}$ e $L_{3}$ sono stati utilizzati per creare il linguaggio $L_{6}$ ; generalizzando questa considerazione possiamo affermare che le operazioni insiemistiche consentono di creare linguaggi regolari complessi a partire da linguaggi regolari semplici. Affinché si possa raggiungere questo obiettivo è indispensabile che il risultato delle operazioni insiemistiche sia sempre un linguaggio regolare, esattamente ciò che intendiamo dimostrare attraverso le proprietà di chiusura.

Nei seguenti paragrafi affronteremo le dimostrazioni riguardanti la chiusura delle seguenti operazioni insiemistiche:

complementazione: se $L$ è un linguaggio regolare, allora anche $\overline{L}$ lo è;
intersezione: se $L_{1}$ e $L_{2}$ sono linguaggi regolari, allora anche $L_{3} = L_{1} \cap L_{2}$ lo è;
unione: se $L_{1}$ e $L_{2}$ sono linguaggi regolari, allora anche $L_{3} = L_{1} \cup L_{2}$ lo è;
differenza: se $L_{1}$ e $L_{2}$ sono linguaggi regolari, allora anche $L_{3} = L_{1} ∖ L_{2}$ lo è.

Accanto alle abituali operazioni insiemistiche i linguaggi formali sono chiusi anche rispetto alle seguenti operazioni:

concatenazione: se $L_{1}$ e $L_{2}$ sono linguaggi regolari, allora anche $L_{3} = L_{1} \circ L_{2}$ lo è;
operatore star di Kleene: se $L$ è un linguaggio regolare, anche $L^{*}$ lo è;
riflessione: se $L$ è un linguaggio regolare, anche $L^{R}$ lo è.

Per dimostrare questi risultati si sfrutterà una conseguenza del teorema di Myhill - Nerode, ossia la relazione di biunivocità esistente tra linguaggi regolari ed accettori a stati finiti. Grazie a questo aspetto è possibile affermare che, dato un linguaggio regolare è possibile costruire un accettore a stati finiti che lo riconosca e viceversa.

Dunque per dimostrare che i linguaggi regolari sono chiusi rispetto ad una particolare operazione basta fornire una procedura che permetta di costruire un automa a stati finiti in grado di riconoscere il linguaggio risultante dall'operazione.

Complementazione di un linguaggio regolare

Dimostreremo che, a partire da un generico linguaggio regolare $L$ riconosciuto da un automa a stati finiti $M$ è possibile costruire un accettore a stati finiti $\overline{M}$ che riconosce il linguaggio $\overline{L}$ . Considerando che ogni linguaggio riconosciuto da una macchina a stati finiti è regolare, concluderemo che $\overline{L}$ è regolare.

Teorema

I linguaggi regolari sono chiusi rispetto all'operazione di complementazione.

Dimostrazione

Si consideri un alfabeto $I$ ed un linguaggio regolare $L \subseteq I^{*}$ . Esiste almeno un automa accettore a stati finiti $M = (Q, I, δ, q_{0}, F \subseteq Q)$ che riconosce il linguaggio $L$ .

Per definizione di complementazione possiamo scrivere $\overline{L} = {x \in I^{*} | x \notin L}$ , da cui deduciamo che nel linguaggio complementare sono comprese tutte le stringhe che non si trovano nel linguaggio $L$ .

L'automa $\overline{M} = (\overline{Q}, \overline{I}, \overline{δ}, {\overline{q}}_{0}, \overline{F} \subseteq \overline{Q})$ accetterà quindi tutte le stringhe di simboli che non saranno accettate da $M$ ; dal punto di vista della struttura dell'automa, possiamo concludere che l'insieme $\overline{F}$ degli stati finali è il complementare dell'insieme $F$ rispetto a $Q$ : $\overline{F} = Q ∖ F$ ; l'insieme degli stati, l'alfabeto d'ingresso, la funzione di transizione e lo stato iniziale sono invece gli stessi dell'automa $M$ .

In conclusione, l'automa $\overline{M}$ si ottiene da $M$ sostituendo l'insieme degli stati finali con il suo complementare rispetto all'insieme degli stati. Abbiamo quindi dimostrato che esiste almeno un accettore a stati finiti in grado di riconoscere $\overline{L}$ , pertanto il linguaggio in questione è regolare.

Esempio

Consideriamo l'insieme $I = {a, b}$ ed il linguaggio $L \subset I^{*}$ costituito da tutte le stringhe di simboli che iniziano con la sequenza $a b$ . L'obiettivo è dimostrare che anche il linguaggio costituito da tutte le stringhe che non iniziano con la sequenza $a b$ è regolare. Costruiamo quindi l'accettore a stati finiti $M = (Q, I, δ, q_{0}, F)$ che riconosce il linguaggio $L$ : L'insieme degli stati di tale automa contiene quattro elementi:

$q_{0}$ è lo stato iniziale;
$q_{1}$ è lo stato che riconosce tutte le stringhe che iniziano con il simbolo $a$ ;
$q_{2}$ è lo stato che riconosce tutte le stringhe che iniziano con la sequenza $a b$ ;
$q_{3}$ è lo stato che riconosce tutte le stringhe che non iniziano con $a$ o che non hanno $b$ come secondo simbolo.

La funzione di transizione è rappresentata dalla tabella sottostante.

	a	b
$\to q_{0}$	$q_{1}$	$q_{3}$
$q_{1}$	$q_{3}$	$q_{2}$
$* q_{2}$	$q_{2}$	$q_{2}$
$q_{3}$	$q_{3}$	$q_{3}$

L'insieme degli stati finali sarà $F = {q_{2}}$ .

L'immagine sottostante mostra il diagramma degli stati dell'automa appena definito.

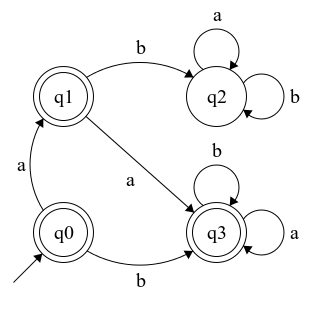
In base a quanto è stato detto in precedenza è possibile costruire l'automa che riconosce il linguaggio complementare a quello dato cambiando solamente l'insieme degli stati finali. Il nuovo insieme $\overline{F}$ è definito come $\overline{F} = Q ∖ F$ e l'automa complementare sarà $\overline{M} = (Q, I, δ, q_{0}, \overline{F})$ .

Il diagramma degli stati per l'automa complementare è visibile nell'immagine sottostante.

Intersezione di linguaggi regolari

In questa sezione dimostreremo che, dati due linguaggi regolari $L_{1}$ e $L_{2}$ , il linguaggio $L = L_{1} \cap L_{2}$ ottenuto dall'intersezione dei due linguaggi è anch'esso regolare.

Teorema

I linguaggi regolari sono chiusi rispetto all'operazione di intersezione.

Dimostrazione

Consideriamo due linguaggi regolari $L_{1} \subseteq I^{*}$ e $L_{2} \subseteq I^{*}$ . Per dimostrare che il linguaggio $L$ ottenuto intersecando i due insiemi è regolare forniremo una procedura che permetterà di costruire un accettore a stati finiti per $L$ . Si nota subito che i due linguaggi sono costruiti a partire dal medesimo alfabeto di partenza: questa scelta è stata operata in quanto la letteratura non è concorde sulle tecniche da applicare in caso gli alfabeti fossero distinti.

Visto che i linguaggi $L_{1}, L_{2}$ sono regolari, ad ognuno di essi sarà associato un accettore a stati finiti: diremo che $M_{1} = (Q_{1}, I, δ_{1}, q_{01}, F_{1})$ è l'accettore che ha $L_{1}$ come linguaggio macchina, $M_{2} = (Q_{2}, I, δ_{2}, q_{02}, F_{2})$ è l'accettore che ha $L_{2}$ come linguaggio macchina.

A partire dai due accettori è possibile costruire un nuovo automa a stati finiti $M = (Q, I, δ, q_{0}, F)$ , in modo che le stringhe riconosciute dall'accettore siano proprio quelle che appartengono al linguaggio $L = L_{1} \cap L_{2}$ .

Vediamo come procedere: per definizione di intersezione, possiamo scrivere che $L = L_{1} \cap L_{2} = {x \in I | (x \in L_{1}) \land (x \in L_{2})}$ ; una stringa $x$ viene quindi accettata dall'automa $M$ quando è accettata da tutti e due gli automi di provenienza.

Un modo per rappresentare la struttura di $M$ è il seguente:

$Q = Q_{1} \times Q_{2}$ : l'insieme degli stati è costituito da coppie ordinate di stati $(q_{1}, q_{2})$ ;
$δ : Q_{1} \times Q_{2} \times I \to Q_{1} \times Q_{2}$ associa ad ogni coppia ordinata di stati e ad ogni simbolo d'ingresso al massimo una coppia ordinata di stati prossimi;
$q_{0} = (q_{01}, q_{02})$ è la coppia ordinata degli stati iniziali;
$F = F_{1} \times F_{2}$ è il prodotto cartesiano degli insiemi degli stati finali.

La funzione di transizione merita un chiarimento: lo stato attuale della macchina $M$ è rappresentato da una coppia ordinata $(q_{1} \in Q_{1}, q_{2} \in Q_{2})$ di stati che sono gli stati attuali in cui si trovano i due accettori $M_{1}$ e $M_{2}$ . $δ (q_{1} \in Q_{1}, q_{2} \in Q_{2}, a \in I)$ associa allo stato attuale della macchina uno stato prossimo in base al simbolo d'ingresso ricevuto. Più precisamente si potrà scrivere: $δ (q_{1}, q_{2}, a) = (δ_{1} (q_{1}, a), δ_{2} (q_{2}, a))$ .

Affinché l'evoluzione dell'automa $M$ conduca ad uno stato finale è necessario che l'esecuzione si arresti in uno stato $(q_{f 1}, q_{f 2})$ in cui $q_{f 1} \in F_{1}$ e contemporaneamente $q_{f 2} \in F_{2}$ . In particolare, quando uno solo dei due stati finali è di accettazione, la stringa d'ingresso si considera non accettata in quanto riconosciuta da un solo automa e non dall'altro, contraddicendo la definizione d'intersezione.

Grazie a questa procedura è stato possibile realizzare un automa a stati finiti $M$ in grado di riconoscere il linguaggio $L = L_{1} \cap L_{2}$ ; dal momento che per tale linguaggio esiste un accettore a stati finiti, possiamo concludere che $L$ è regolare.

Il teorema è dunque dimostrato.

Esempio

Questo esempio illustrerà un'applicazione della tecnica impiegata nella dimostrazione del teorema soprastante. I linguaggi coinvolti sono costruiti a partire da un alfabeto $I = {0, 1}$ .

Consideriamo il linguaggio regolare $L_{1} \subset I^{*}$ costituito da tutte le stringhe che contengono un numero pari di simboli "1". Consideriamo poi un secondo linguaggio regolare $L_{2} \subset I^{*}$ costituito da tutte le stringhe che contengono almeno due simboli "0" consecutivi.

Possiamo affermare che il linguaggio $L = L_{1} \cap L_{2}$ è costituito da tutte le stringhe che contengono un numero pari di simboli "1" e almeno due simboli "0" consecutivi; dimostreremo che tale linguaggio è regolare costruendo un automa riconoscitore attraverso la tecnica impiegata nella dimostrazione precedente.

Prima di presentare l'accettore riguardante il linguaggio $L$ vale la pena di mostrare gli accettori dei due linguaggi $L_{1}$ e $L_{2}$ .

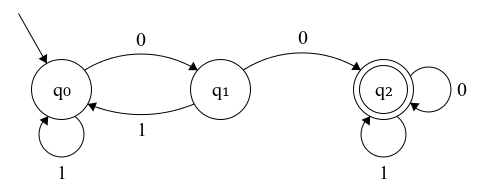
Nel caso del linguaggio costituito da stringhe con un numero pari di simboli "1", il diagramma degli stati per l'automa che lo riconosce è visibile nell'immagine sottostante.

Il linguaggio costituito da stringhe che contengono una sequenza di almeno due simboli "0" è associato all'accettore illustrato nel diagramma degli stati visibile di seguito.

Il seguente diagramma a stati è suddiviso in tre parti: in alto è visibile il diagramma a stati dell'automa che riconosce le stringhe contenenti almeno due zeri, sulla destra è visibile l'accettore che riconosce le stringhe con un numero pari di simboli "1", mentre nella zona centrale è presente il diagramma a stati dell'automa che accetta il linguaggio $L$ , costruito seguendo il metodo proposto nella dimostrazione del teorema.

Abbiamo in questo modo dimostrato l'esistenza di un accettore a stati finiti che ha $L$ come linguaggio macchina; come conseguenza il linguaggio in questione deve per forza essere regolare.

Unione di linguaggi regolari

A rigor di logica non sarebbe necessario presentare una dimostrazione per il caso dell'unione insiemistica di linguaggi regolari, in quanto è possibile formulare l'unione di due insiemi utilizzando l'intersezione e la complementazione.

Dati due linguaggi regolari $L_{1}$ e $L_{2}$ e considerando le leggi di De Morgan è possibile scrivere $L_{1} \cup L_{2} = \overline{({\overline{L}}_{1} \cap {\overline{L}}_{2})}$ . Applicando poi i due teoremi dimostrati in precedenza si può dedurre che i linguaggi regolari sono chiusi anche rispetto all'unione.

Nonostante ciò, dal punto di vista didattico è indubbiamente interessante provare a dimostrare il teorema riguardante l'unione di linguaggi regolari sfruttando una tecnica simile a quella presentata per l'intersezione, semplicemente adattando la definizione dell'automa prodotto alle caratteristiche dell'operazione di unione.

Teorema

I linguaggi regolari sono chiusi rispetto all'operazione di unione.

Dimostrazione

Consideriamo due linguaggi regolari $L_{1} \subseteq I^{*}$ e $L_{2} \subseteq I^{*}$ . Per definizione, l'unione insiemistica dei due linguaggi sarà $L = L_{1} \cup L_{2} = {x | (x \in L_{1}) \lor (x \in L_{2})}$ .

Dato che i due linguaggi sono regolari, esisteranno anche due accettori a stati finiti $M_{1} = (Q_{1}, I, δ_{1}, q_{01}, F_{1})$ e $M_{2} = (Q_{2}, I, δ_{2}, q_{02}, F_{2})$ .

Per dimostrare l'esistenza di un automa accettore in grado di riconoscere il linguaggio $L$ procederemo in modo analogo a quanto fatto nella dimostrazione riguardante l'intersezione insiemistica, ma dovremo prestare attenzione al modo in cui definiremo gli stati finali. Infatti, mentre nel caso dell'intersezione uno stato di accettazione richiedeva che entrambi gli stati di partenza fossero di accettazione, in questo caso basterà che uno solo dei due, oppure tutti e due, siano stati finali.

Grazie a questa considerazione è possibile identificare le caratteristiche dell'automa $M = (Q, I, δ, q_{0}, F)$ in grado di riconoscere il linguaggio $L$ :

$Q = Q_{1} \times Q_{2}$ ;
$δ : Q_{1} \times Q_{2} \times I \to Q_{1} \times Q_{2}$ ;
$q_{0} = (q_{01}, q_{02})$
$F = {(q_{A}, q_{B}) | (q_{A} \in F_{1}) \lor (q_{B} \in F_{2})} = (F_{1} \times Q_{2}) \cup (Q_{1} \times F_{2})$ .

Procedendo in modo analogo a quanto fatto nel caso del teorema riguardante l'intersezione è possibile dimostrare che l'accettore appena descritto ha come linguaggio macchina proprio $L$ .

In conclusione, siccome $L$ è un linguaggio formale associato ad un accettore a stati finiti, dev'essere necessariamente un linguaggio regolare.

Esempio

Presentiamo un esempio di applicazione del teorema in cui si costruirà l'accettore a stati finiti dell'unione di due linguaggi regolari definiti sull'alfabeto $I = {0, 1}$ . Più precisamente, il linguaggio $L_{1}$ contiene tutte le stringhe che iniziano con la sequenza "10", mentre il linguaggio $L_{2}$ è formato da tutte le stringhe che terminano con la sequenza "01". L'unione insiemistica dei due linguaggi, indicata con $L$ , è un linguaggio che contiene tutte le stringhe che iniziano con la sequenza "10" oppure che finiscono con la sequenza "01". Il diagramma a stati del linguaggio $L_{1}$ è presentato di seguito.

Qui sotto è visibile il diagramma a stati per il linguaggio $L_{2}$ .

Applicando la tecnica di costruzione dell'automa prodotto, si ottiene un automa accettore per il linguaggio $L = L_{1} \cup L_{2}$ che ha il diagramma degli stati sottostante.

Come si può notare osservando il diagramma, vi sono alcuni stati che non vengono visitati durante l'evoluzione dell'automa; ciò significa che l'applicazione della tecnica dell'automa prodotto non conduce, in generale, ad un automa a stati minimi. In generale, quindi, è consigliabile ridenominare gli stati e sottoporre ad ottimizzazione l'automa ottenuto mediante questo procedimento.

Differenza di linguaggi regolari

Per la dimostrazione della differenza di due linguaggi regolari non sarà necessario produrre un accettore a stati finiti, bensì verranno sfruttate le proprietà delle operazioni già esaminate per estendere la chiusura anche al caso dell'operazione di differenza.

Teorema

I linguaggi regolari sono chiusi rispetto all'operazione di differenza.

Dimostrazione

Siano dati due linguaggi formali $L_{1} \in I^{*}$ e $L_{2} \in I^{*}$ . La differenza tra i due insiemi è un linguaggio $L$ con la seguente caratteristica: $L = L_{1} ∖ L_{2} = {s | (s \in L_{1}) \land (s \notin L_{2})}$ .

Le stringhe che fanno parte del linguaggio $L$ appartengono a $L_{1}$ e al complementare di $L_{2}$ ; potremo quindi scrivere $L = L_{1} \cap {\overline{L}}_{2}$ .

Dato che questa espressione contempla unicamente linguaggi regolari ed operazioni per le quali è già stata dimostrata la chiusura, possiamo concludere che il linguaggio $L$ è regolare. È quindi dimostrato che i linguaggi regolari sono chiusi rispetto all'operazione di differenza.

Differenza simmetrica di linguaggi regolari

In modo analogo a quanto visto per la differenza di linguaggi regolari, si può dimostrare che anche la differenza simmetrica è un'operazione chiusa rispetto ai linguaggi regolari.

Teorema

I linguaggi regolari sono chiusi rispetto all'operazione di differenza simmetrica.

Dimostrazione

Siano dati due linguaggi $L_{1} \in I^{*}$ e $L_{2} \in I^{*}$ . Per definizione di differenza simmetrica possiamo scrivere $L = L_{1} △ L_{2} = (L_{1} ∖ L_{2}) \cup (L_{2} ∖ L_{1})$ ; questa formulazione della differenza simmetrica contiene solamente linguaggi regolari ed operazioni insiemistiche per le quali è già stata dimostrata la chiusura. Ne possiamo concludere che il linguaggio $L$ è regolare e, per la generalità di tale risultato, che il teorema è dimostrato.

Conseguenze pratiche delle proprietà di chiusura

Le tecniche impiegate durante la dimostrazione di alcune proprietà di chiusura (complementazione, unione e intersezione), meritano un approfondimento; infatti, sebbene esse siano state introdotte con l'obiettivo di offrire una dimostrazione costruttiva dei teoremi, la loro utilità pratica è di gran lunga maggiore.

Nelle dimostrazioni in questione è stato evidenziato come linguaggi dotati di caratteristiche complesse possano essere formati a partire da linguaggi più semplici; sono state inoltre presentate delle tecniche di progettazione degli accettori a stati finiti che consentono di costruire accettori complessi a partire da accettori più semplici.

Questo approccio risulta, in linea di massima, più flessibile rispetto alla costruzione di automi ad-hoc; inoltre, sfruttando gli algoritmi di minimizzazione degli stati già esaminati nella lezione precedente è facile ricondurre i nuovi accettori così progettati alle loro forme canoniche.

L'applicazione di queste tecniche permette quindi, in un sol colpo, di dimostrare la regolarità dei linguaggi e di costruire automi a stati finiti in grado di riconoscerli.

Lezione precedente: Minimizzazione degli stati di un automa

Corso: Materia:Informatica Teorica

Prossima lezione: Automa a pila

Proprietà di chiusura dei linguaggi regolari

Indice

Introduzione

Complementazione di un linguaggio regolare

Teorema

Dimostrazione

Esempio

Intersezione di linguaggi regolari

Teorema

Dimostrazione

Esempio

Unione di linguaggi regolari

Teorema

Dimostrazione

Esempio

Differenza di linguaggi regolari

Teorema

Dimostrazione

Differenza simmetrica di linguaggi regolari

Teorema

Dimostrazione

Conseguenze pratiche delle proprietà di chiusura

Menu di navigazione

Proprietà di chiusura dei linguaggi regolari

Introduzione

Complementazione di un linguaggio regolare

Teorema

Dimostrazione

Esempio

Intersezione di linguaggi regolari

Teorema

Dimostrazione

Esempio

Unione di linguaggi regolari

Teorema

Dimostrazione

Esempio

Differenza di linguaggi regolari

Teorema

Dimostrazione

Differenza simmetrica di linguaggi regolari

Teorema

Dimostrazione

Conseguenze pratiche delle proprietà di chiusura

Menu di navigazione

Ricerca