Studio dell' impulso d'emissione per testa acustica di vettore subacqueo tracciabile

Template:Risorsa La lezione è indirizzata al dimensionamento dell'impulso emesso da una testa acustica di un vettore subacqueo tracciabile in modo che durante la trasmissione questo non provochi emissioni spurie superiori a $-80dB$, rispetto al livello indice del vettore stesso, nella banda $20kHz-30kHz$ destinata a vettori operativi.

Esposizione dei valori di specifica per l'impulso

Le caratteristiche dell'impulso dovranno soddisfare le seguenti specifiche:

• a) Frequenza di trasmissione $fo:fo=50kHz$
• b) Durata impulso :$1.5ms.$
• c) Tempo di ripetizione impulsi: $1s.$
• d) Livello indice di trasmissione: $195dB/\mu Pa$
• e) Livello spurie: in banda $f1-f2$ $(f1=20kHz;f2=30kHz)<-80dB$ rispetto al livello indice di $195dB/\mu Pa$ ( circa $115dB/\mu Pa)$

Spettro di un generico impulso rettangolare di sinusoidi

Se la testa acustica emette un impulso rettangolare, pacchetto di sinusoidi a $50kHz$ della durata di $1.5ms$, abbiamo la coppia della trasformata di Fourier così come mostrato nelle figure 1 e 2:

figura 1

figura 2

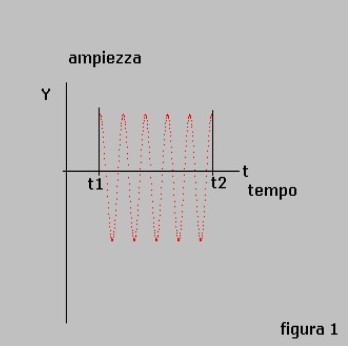
L'impulso di figura 1, funzione del tempo, è definibile matematicamente secondo l'espressione:

$Y=0pert1>t>t2$

$Y=A\cdot \cos (\omega ot)pert1\le t\le t2$

dove $\omega o=2\pi foconfo$ = frequenza dell'onda dell'impulso. Template:Clear

La $G(\omega )$ è caratterizzata dal valore assoluto della nota funzione $\mathrm{sen}x/x$ con $\omega$ variabile da $-\mathrm{\infty }a+\mathrm{\infty }$ lo spettro si estende per frequenze superiori ed inferiori a $\omega o$ secondo l'algoritmo:

$G(\omega )=\frac{A(t_2-t_1)}{2}\left|\frac{\sin \left[\frac{(\omega -{\omega }_0)(t_2-t_1)}{2}\right]}{\left[\frac{(\omega -{\omega }_0)(t_2-t_1)}{2}\right]}\right|$

Per semplificare l'esposizione assumiamo:

• $A=2/(t2-t1)$
• $t2-t1=1.5ms$
• $\omega o=6.28\cdot 50000Hz$

per $\omega =\omega o$ abbiamo:

$G(\omega )=1$.

Dall'algoritmo risulta inoltre:

• Il livello di $G(\omega )$ per $(f1=20000Hz)=0.0005$
• Il livello di $G(\omega )$ per $(f2=30000Hz)=0.0005$

Il livello sp di spurie in tutta la banda $f2-f1=10000Hz$ è pertanto:

$sp=(0.0005)\cdot \sqrt[]{10000}=0.05$ pari a $26dB$ sotto il massimo di

$G(\omega )=1$.

Controllo sperimentale del livello di spurie dell'impulso rettangolare

Il controllo del livello di spurie emerso dai calcoli precedenti è fattibile con il circuito di figura 3 che, una volta validato, sarà utile per la verifica dei valori imposti da specifica:

figura 3

Come si vede da figura 3, con l'ampiezza dell'impulso di $13Vpp$, il livello di spurie all'uscita del filtro è di $0.32Vpp$ che, data l'attenuazione di $9dB$ del filtro, corrisponde ad un livello di spurie pari a : $0.32Vpp+9dB=0.9Vpp$ con un rapporto di:

$sp=20\cdot Log(13Vpp/0.9Vpp)=23dB.$

Il rapporto tra il livello del segnale e le spurie ora misurato è inferiore al valore calcolato in precedenza che riporta invece $sp=26dB$, una differenza di $3dB$ dovuta sia all'incertezze di misura sia al rilievo in valori di picco su inviluppi di spurie in banda.

Il generatore degli impulsi

La caratteristica principale del circuito di figura 3 consiste nella particolare struttura del generatore degli impulsi alla frequenza di $50000Hz$ il cui stadio finale di potenza è riportato in figura 4:

figura 4

Il circuito è stato adottato per la possibilità di parzializzare il segnale rettangolare di pilotaggio sì da controllare l'ampiezza del segnale sinusoidale d'uscita.

Verifica della legge di variazione d'ampiezza dell'impulso di figura 1

Per sagomare opportunamente l'impulso di figura 1 affinché si abbia un abbattimento delle spurie nella banda $20kHz;30kHz$ è necessario operare sugli intervalli "to" del segnale di pilotaggio di figura 3b con i quali si controlla il livello dell'impulso per variarne il profilo nei tempi di ascesa e discesa.

La variazione d'ampiezza dell'impulso di figura 1, in funzione della larghezza degli scalini "to" deve seguire ,secondo la trasformata di Fourier, l'andamento della frequenza fondamentale dello spettro:

$A=(2/\pi )\mathrm{sen}(\pi k/2)$

dove $k=to/(T/2)$ .

figura 5

Un confronto tra la funzione teorica e l'andamento sperimentale rilevato sul prototipo è riportato in figura 5: come si vede il generatore segue la legge voluta ed è a garanzia che il successivo processo di profilazione dell'impulso seguirà la funzione di modulazione assegnata. Template:Clear

La funzione di mascheramento

La funzione di mascheramento necessaria alla modifica dei valori di "to" al fine di ottenere il profilo voluto dell'impulso, per abbattere lo spettro di $G(\omega )$ nella banda $20kHz;30KHz.$ è dovuta ad Hanning:

$Wn=(1/2)[1-\cos (2\pi nN)]$

Opportunamente applicata la funzione di mascheramento al generatore d'impulsi, con apposito modulatore di larghezza, si ottiene il risultato mostrato in figura 6:

figura 6

In questo caso il rapporto tra l'ampiezza dell'impulso ( $13Vpp$ al centro ) e il livello delle spurie all' ingresso del filtro è:

$sp=20\cdot Log(13Vpp/0.00044Vpp)-9dB=80dB$ come richiesto da specifica.

Bibliografia

A. Papoulis, The Fourier integral and its applications, Mc Graw_hill, New York, 1062

F.E. TERMAN, Manuale di ingegneria radiotecnic, A. Martello editore Milano, 1960

International Rectifier, Hexfet databook, IR , 1983